Question

Решите , в пропуски нужно вставить числа даю

Answer 1

1) 8, 24, 2, 2

2) 2, 25, 1, - 2, 2, 2

3) 1

Объяснение:

1) Реши уравнение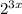 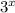$2^{3x}$ * $3^{x}$ = 576

Так как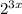 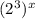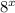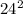$2^{3x}$ = $(2^{3})^{x}$ = $8^{x}$, $24^{2}$ = 576, тогда уравнение можно записать в

виде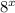 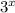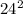$8^{x}$ * $3^{x}$ = $24^{2}$ или в виде $24^{x}$ = $24^{2}$

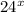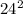
x = 2

ответ: 2

2) Реши уравнение $3^{x+1}$ - 2 * $3^{x - 2}$ = 25

Вынося в левой части за скобки общий множитель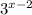 $3^{x-2}$, получаем $3^{x-2}$($3^{3}$-

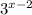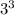2) = 25,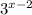 $3^{x-2}$ * 25 = 25, откуда 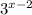$3^{x-2}$ = 1, x - 2 = 0,

х = 2

ответ: 2

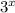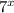3) Реши уравнение $3^{x}$ = $7^{x}$.

Так как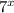 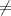$7^{x}$$\neq$ 0, то уравнение можно записать в виде 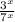$\frac{3^{x} \\}{7^{x} }$ = 1, откуда

$(\frac{3}{7})^{x}$ = $(\frac{3}{7})^{0}$, x = 0.

ответ: 0