![\left\{\begin{array}{l}x-2y+3z-6=0\\3x-2y-5z-6=0\end{array}\right\\\\\\a)\ \ [\, \vec{n}_1\times \vec{n}_2\, ]=\left|\begin{array}{ccc}i&j&k\\1&-2&3\\3&-2&-5\end{array}\right|=16\vec{i}+14\vec{j}+4\vec{k}\\\\\\\vec{s}=\lambda \, [\, \vec{n}_1\times \vec{n}_2\, ]=\dfrac{1}{2}\cdot (16;14;4)=(8;7;2)](/tpl/images/2056/6063/a8029.png)

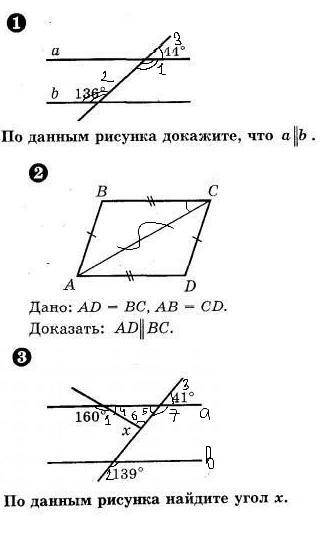
1. ∠1 и ∠3 смежные, значит ∠1 = 180° - ∠3 = 180° - 44° = 136°
∠1 и∠2 внутр. накрест лежащие углы, они равны между собой по 136° => a параллельно b
2. рассмотрим ΔABC и ΔADC.
они равны по 3 признаку, так как AC общая сторона, AD = BC и AB = CD
∠BCA = ∠DAC (как внутр. накрест лежащие углы), а из этого следует, что AD параллельно BC
3. обозначим на рисунке ∠4, ∠5, ∠6 и ∠7
∠7 = 180° - ∠3 = 180° - 41° = 139°, следовательно ∠7 = ∠3, значит a параллельно b
∠5 = ∠3 = 41° (как вертикальные)
∠4 = 180° - ∠1 = 180° - 160° = 20°
и ∠6 = 180° - ∠4 - ∠5 = 180° - 20° - 41° = 119°
следовательно угол, обозначенный как x, равен 180° - ∠6 = 180° - 119° = 61°