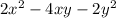Алгоритм (решения линейных уравнений) Раскрыть скобки в каждой части уравнения (если нужно). Неизвестные собрать в левой части уравнения, известные в правой части уравнения. ( При переносе слагаемых из одной части уравнения в другую знак «+» меняем на “ –“, а знак “ – “ на «+».) В каждой части уравнения приведи подобные слагаемые. Неизвестное найди, как неизвестный множитель ( произведение подели на известный множитель). Алгоритм. Решение линейных неравенств. Раскрыть скобки (если нужно). Неизвестные перенести в левую часть неравенства, известные в правую часть. ( При переносе знаки перед слагаемыми изменить на противоположные “-“ на “+“; “+“ на “-“; знак неравенства сохраняется). В каждой части привести подобные слагаемые, получаем неравенство вида: ax < b или ax > b или ax £ b или ax ³ b. Чтобы найти x, число (b) стоящие в правой части разделить на коэффициент при x (a), причём, если a>o, то знак неравенства сохраняется, если a<0, то знак меняется на противоположный ( “<” на “>”; “>” на “<”; “£” на “³”; “³” на “£”). Решение изобразить на числовой прямой и ответ записать промежутком.
Алгоритм (решения линейных уравнений) Раскрыть скобки в каждой части уравнения (если нужно). Неизвестные собрать в левой части уравнения, известные в правой части уравнения. ( При переносе слагаемых из одной части уравнения в другую знак «+» меняем на “ –“, а знак “ – “ на «+».) В каждой части уравнения приведи подобные слагаемые. Неизвестное найди, как неизвестный множитель ( произведение подели на известный множитель). Алгоритм. Решение линейных неравенств. Раскрыть скобки (если нужно). Неизвестные перенести в левую часть неравенства, известные в правую часть. ( При переносе знаки перед слагаемыми изменить на противоположные “-“ на “+“; “+“ на “-“; знак неравенства сохраняется). В каждой части привести подобные слагаемые, получаем неравенство вида: ax < b или ax > b или ax £ b или ax ³ b. Чтобы найти x, число (b) стоящие в правой части разделить на коэффициент при x (a), причём, если a>o, то знак неравенства сохраняется, если a<0, то знак меняется на противоположный ( “<” на “>”; “>” на “<”; “£” на “³”; “³” на “£”). Решение изобразить на числовой прямой и ответ записать промежутком.
1)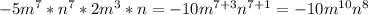
ответ: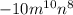
2)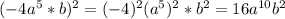
ответ: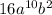
3)
ответ: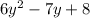
4)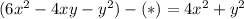
ответ: