26,
т.к. по условию в графу ответа надо писать
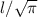
Объяснение:
Из условия ни разу не ясно, что есть такое некая непонятная "его длина".
Но по всей видимости,
а) это диаметр условной окружности, которую образует Кольцевая линия.
б) это (ну, блин, грамотеи!) длина окружности, которую образует Кольцевая линия.
а) Найдем диаметр условной окружности, которую образует Кольцевая линия.
Обозначим её как d.
Площадь Центрального района S можно вычислить следующим образом:
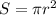
где r - это радиус условной окружности Кольцевой, или половина диаметра, т.е. d/2. Отсюда.
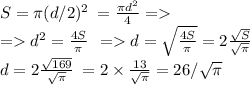
б) Найдем длину окружности, которую образует Кольцевая линия. Обозначим её как l.
Длина окружности равна
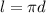
где d - условный диаметр (см. (а)).
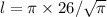
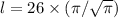
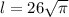
Согласно требованиям задачи в ответ записываем
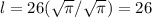
т.е.
ответ: 26
Объяснение:
0\hfill\\x-3>0\hfill\\x-3\ne1\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}x>-1\hfill\\x>3\hfill\\x\ne4\hfill\\\end{gathered}\right.\hfill\\\boxed{x\in(3;+\infty)}\hfill\\\end{gathered}\]" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=%5C%5B%5Cbegin%7Bgathered%7D2%29%5C%3B%5C%3B%7B%5Clog_%7Bx-3%7D%7D%28x%2B1%29%5Chfill%5C%5C%5Cleft%5C%7B%5Cbegin%7Bgathered%7Dx%2B1%3E0%5Chfill%5C%5Cx-3%3E0%5Chfill%5C%5Cx-3%5Cne1%5Chfill%5C%5C%5Cend%7Bgathered%7D%5Cright.%5CLeftrightarrow%5Cleft%5C%7B%5Cbegin%7Bgathered%7Dx%3E-1%5Chfill%5C%5Cx%3E3%5Chfill%5C%5Cx%5Cne4%5Chfill%5C%5C%5Cend%7Bgathered%7D%5Cright.%5Chfill%5C%5C%5Cboxed%7Bx%5Cin%283%3B%2B%5Cinfty%29%7D%5Chfill%5C%5C%5Cend%7Bgathered%7D%5C%5D" title="\[\begin{gathered}2)\;\;{\log_{x-3}}(x+1)\hfill\\\left\{\begin{gathered}x+1>0\hfill\\x-3>0\hfill\\x-3\ne1\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}x>-1\hfill\\x>3\hfill\\x\ne4\hfill\\\end{gathered}\right.\hfill\\\boxed{x\in(3;+\infty)}\hfill\\\end{gathered}\]">
смотри в прикреплённом файле