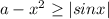
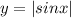расположен выше оси ОХ. 
.
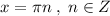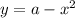- это параболы , ветви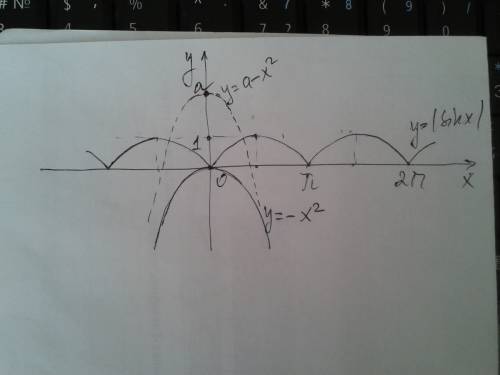
1
Объяснение:
Угол наклона прямой в координатной плоскости изменяется в промежутке [0; π) за исключением π/2, то есть по значению тангенса можно однозначно определить угол. Вспомним, что прямые параллельны, если соответственные углы равны. Если принять за секущую ось Ox, то можно сравнить углы наклона. А для этого уже достаточно сравнить их тангенсы!
Тангенс угла наклона касательной можно найти с производной — это значение производной в данной точке. Тангенс угла наклона прямой — это коэффициент перед x. Тогда:
— если подставить вместо x какое-то значение, получим тангенс угла наклона касательной. Тангенс угла наклона прямой — это 1 (y = 1*x + 8). Поэтому, чтобы прямые были параллельны, нужно приравнять производную и тангенс угла наклона прямой:
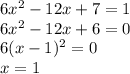
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)