По формулам приведения:
если в тригонометрической формуле встречается выражение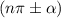 , где
, где 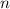 — целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 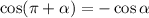 (минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение
(минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение 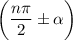 , где
, где 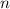 — целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 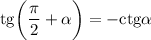 (минус, потому что общий угол будет находиться во второй четверти).
(минус, потому что общий угол будет находиться во второй четверти).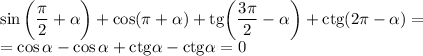
6x^2-7x+2>0
6x^2-3х-4х+2>0
3х*(2х-1)-2(2х-1)>0
(3х-2)*(2х-1)>0
{3х-2>0
{2х-1>0
{3х-2<0
{2х-1<0
{х>2/3
{х>1/2
{х<2/3
{х<1/2
Х принадлежит (2/3, +бесконечность)
Х принадлежит (-бесконечность, 1/2)
Х принадлежит (-бесконечность, 1/2) U Х принадлежит (2/3, +бесконечность)
в)
8x^2+10x-3 <0
8x^2+12-2х-3<0
4х*(2х+3)-(2х+3)<0
(4х-1) *(2х+3)<0
{4х-1<0
{2х+3>0
{4х-1>0
{2х+3<0
{х<1/4
{х>-3/2
{х>1/4
{х<-3/2
Х принадлежит (-3/2, 1/4)
Х принадлежит Ø
Х принадлежит (-3/2, 1/4)