1) Вероятность того, что по мишени не попали ни одного раза, равна
P = (1-0.7) * (1-0.8) = 0.06
Вероятность того, что мишень будет поражена хотя бы одним выстрелом, равна
P* = 1 - P = 1 - 0.06 = 0.94
2) Вероятность того, что мишень не будет поражена на одним из выстрелов, равна (1-0.7)*(1-0.8) = 0.06
Задание 2.
Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:
P(A+B) = P(A) + P(B) - P(AB) = 0.3 + 0.8 - 0.1 = 1
Следовательно, A+B=∪ — достоверно.
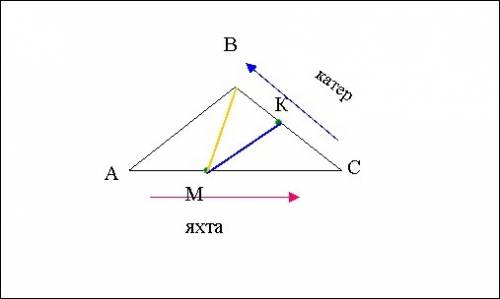
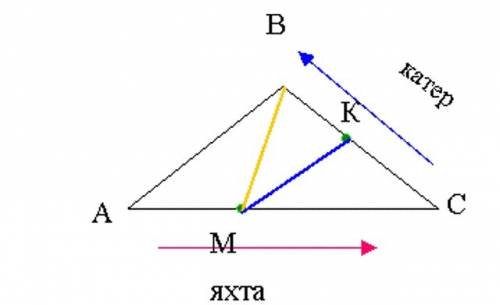
Чертёж ниже, кликни по нему мышкой.
Яхта села на мель в точке М, поэтому будем искать расстояние ВМ, которое пройдёт лодка к яхте и расстояние КМ, которое пройдёт катер к яхте.
1). Будем находить длины сторон треугольников по теореме косинусов, поэтому сначала из ∆АВС найдём cos<C
АВ2 = ВС2 + АС2 - 2*ВС*АС*cos<C
отсюда
cos<C = (ВС2 + АС2 - АВ2)/(2*ВС*АС)
cos<C = (702 + 902 - 702)/(2*70*90)=
= 8100/12600 = 81/126 = 9/14
cos<C = 9/14
2) АМ = СК = 10 * 2 = 20 км
МС = АС - АМ = 90 - 20 = 70 км
3) Из ∆МКС найдём длину стороны КМ по т. косинусов
КМ2 = МС2 + СК2 - 2*МС*СК*cos<C
КМ2 = 702 + 202 - 2 * 70 * 20 * 9/14 = 4900 + 400 - 1800 = 3500
КМ = √3500 = 10√35 км
4) Из ∆МВС найдём длину стороны ВМ:
ВМ2 = МС2 + СВ2 - 2*МС*СВ*cos<C
ВМ2 = 702 + 702 - 2 * 70 * 70 * 9/14 = 9800 - 9800 * 9/14 =
= 9800 - 9800 * 9/14 = 9800 - 6300 = 3500
ВМ = √3500 = 10√35 км
5) Расстояния ВМ, которое пройдёт лодка для оказания и расстояние КМ, которое пройдёт катер для оказания яхте равны между собой: ВМ = КМ = 10√35 км.
Скорости тоже равны по 20км/ч
Значит, и время будет одинаковое, 10√35 км : 20 км/ч = √35/2 ч ≈ 2,9ч, т.е. лодка и катер к яхте прибудут одновременно.
ответ: лодка и катер к яхте прибудут одновременно.
-10x-4y=-28 (умножено на -2)
Складываем
-7x=-14
x=2
y=2