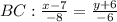 ,
,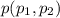 .
. в прямоугольной системе координат, то вектор
в прямоугольной системе координат, то вектор  является вектором нормали данной прямой.
является вектором нормали данной прямой.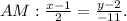
Уравнение 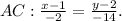
Или в общем виде 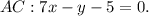
Нормальный вектор стороны АС 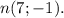 , а для высоты ВН он будет направляющим:
, а для высоты ВН он будет направляющим:
Уравнение высоты 
Или в общем виде: -х + 7 = 7у + 42,
х + 7у + 35 = 0.
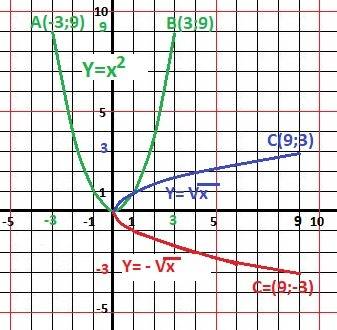
ладададщаащвщащащащащащ