Сначала всё обозначим:
ширина бассейна по условию х;
длина бассейна х+6;
ширина прямоугольника,в котором находится бассейн, х + 1 (добавилось по 0,5 м с каждой стороны за счёт дорожки);
длина этого же прямоугольника х + 7 (также добавилось по 0,5 м с двух сторон за счёт дорожки).
Дальше из площади большого прямоугольника вычитаем площадь малого(бассейн) и получаем разницу 15 кв.метров - площадь всей дорожки по условию:
(x+7) *(x+1) - (x+6) * x = 15
x^2 + x + 7x - x^2 - 6x = 15 2x=8 x=4(ширина бас.); 4+6=10 (длина бас.).
Найдем дискриминант квадратного уравнения:
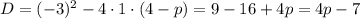
1) D > 0; 4p - 7 > 0 откуда p>7/4 - квадратное уравнение имеет два корня
2) D = 0; 4p - 7 =0 откуда p=7/4 - квадратное уравнение имеет один корень
3) D < 0 ⇒ p < 7/4 - квадратное уравнение не имеет корней.
1.1) {а, л, г, е, б, р}
1.2) {2, 4, 6, 8}
1.3) {1, 3, 5, 7, 9}
1.4) {2, 3, 5, 7}
2.1) A={1, 2, 3, 4, 6, 12}
2.2) B={1, 2, 3, 5, 6, 10, 15, 30}
2.3) X={-6, -3, -2, -1, 1, 2, 3, 6}
2.4) F={2,3}