
Воспользуемся методом введения вс угла:
1) √2sinx + √6cosx = ...
√(2 + 6) = √8 = 2√2
... = √8(sinx·cos(arccos(1/2) + cosx·sin(arccos(1/2)) = √8sin(x + π/3)
-1 ≤ sin(x + π/3) ≤ 1
-√8 ≤ √8sin(x + π/3) ≤ √8 ⇒ max = √8;
2) 3sinx + 4cosx = 5(sinx·cos(arccos(3/5) + cos·sin(arccos(3/5)) = 5sinx(x + arccos(3/5))
-1 ≤ sinx(x + arccos(3/5)) ≤ 1
-5 ≤ 5sinx(x + arccos(3/5)) ≤ 5 ⇒ max = 5
3) 2siny - 5cosy = √29(siny·cos(arccos(2/√29) + cosy·sin(arccos(5/√29)
max = √29
P.s.: нужно воспользоваться тем, что синус принимает значения на отрезке [-1; 1], а также, что выражение вида Asinx + Bcosy можно привести к виду:
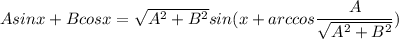
Для начала делаем замену
такая замена делается, когда идентичных скобок 2, 4 , 8, 16 итд
ищем среднее арифметическое констант в скобках
(+2 - 5 + 3 - 4) / 4 = -1
делаем замену y = x-1
заменяем
x+2 = y + 3
x - 5 = y - 4
x + 3 = y + 4
x - 4 = y - 3
(y+3)(y-4)(y+4)(y-3) = -6
(y^2 - 9)(y^2 - 16) = -6
y^2 - 9 = z
z(z-7) = - 6
z^2 - 7z + 6 = 0
D=49 - 24 = 25
z12=(7 +- 5)/2 = 1 6
y^2 - 9 = z
1/ y^2-9 = 1
y^2 = 1 + 9 = 10
y12=+-√10
2/ y^2 - 9 = 6
y^2 = 15
y34 = +-√15
(ну можно полученные игреки здесь сложить они = 0 и потом прибаваить четыре единицы, но доделаем полностью)
y = x -1
x = 1 + y
x12 = 1 +- √10
x34 = 1 +- √15
итого 4 корня
сумма корней x1 + x2 + x3 + x4 = 1 +√10 + 1 + √15 + 1 - √10 + 1 - √15 = 4
ответ 4