А)3(х+2у)-2(3х-у)+4=-3х+8у+4.
в)LP+MS+EN-MN-PL+SE=S°
A2. Найдите значение выражения 2 – tg2x · cos2 x,если sin х = 0,2
1) 1,2 2) 1,96 3) 1,04 4) 1,6
А3. У выражение sin2α ·cos4α - sin6α + sin4α · cos2α
1) sin2α - sin6α 2) -2sin6α 3) 0 4)cos2α – sin6α
А4. Найдите значение выражения √2 · sin22,5 ۫ · cos22,5 ۫
1) 1 2) √2 3) √2/2 4) 0,5
А5. У выражение sin(α – β) + 2 cosα · sinβ
1) cos(α + β) 2) cos(α – β) 3) sin(α + β) 4) sin(α – β)
Объяснение найти правильный ответ
A2. Найдите значение выражения 2 – tg2x · cos2 x,если sin х = 0,2
1) 1,2 2) 1,96 3) 1,04 4) 1,6
А3. У выражение sin2α ·cos4α - sin6α + sin4α · cos2α
1) sin2α - sin6α 2) -2sin6α 3) 0 4)cos2α – sin6α
А4. Найдите значение выражения √2 · sin22,5 ۫ · cos22,5 ۫
1) 1 2) √2 3) √2/2 4) 0,5
А5. У выражение sin(α – β) + 2 cosα · sinβ
1) cos(α + β) 2) cos(α – β) 3) sin(α + β) 4) sin(α – β)
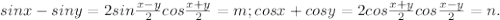
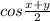. Выразим его из обоих равенств:
.
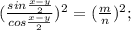
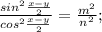
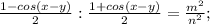
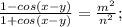
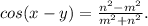
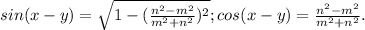
А)3х+6у-6х+у+4= -3х+7у+4
В) я не знаю