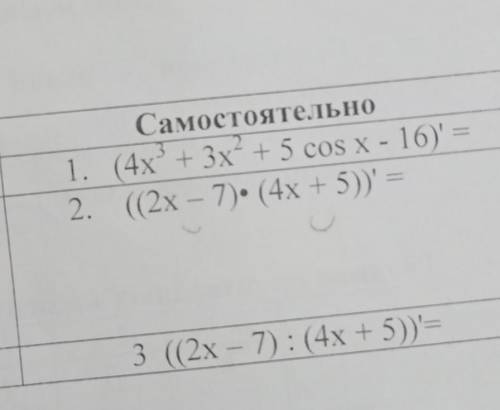
1)
30% числа k = 0,3a
35% числа p = 0,35p
0,3k > 0,35p на 20
Первое уравнение:
0,3k - 0,35p = 20
2)
20% числа k = 0,2а
30% числа p = 0,3р
0,3р > 0,2k на 8
Второе уравнение:
0,2k + 8 = 0,3p
3)
Решаем систему.
{0,3k-0,35р = 20
{0,2k - 0,3р = - 8
Первое умножим на 2, а второе умножим на (-3)
{0,6k-0,7р = 40
{-0,6k+0,9р = 24
Сложим
0,6k-0,7р -0,6k+0,9р = 40+24
0,2р = 64
р = 64 : 0,2
р = 320
В первое уравнение 0,3k - 0,35p = 20 подставим р = 320.
0,3k - 0,35·320 = 20
0,3k - 112 = 20
0,3k = 112 + 20
0,3k = 132
k = 132 : 0,3
k = 440
ответ: k = 440;
р = 320.
Объяснение: ( ^ знак степени)
y'=4*3x^2 +3*2x -5sinx =12x^2 +6x -5sinx
(u*v)'=u'v+u*v', y'=2*(4x+5) + (2x-7)*4=8x+10+8x-28=16x-18
(u/v)'=u'v-uv' /v^2, (2x-7/ 4x+5)'=(2*(4x+5) -(2x-7)*4) /(4x+5)^2 =
(8x+10-8x+28) /(4x+5)^2= 38/ (4x+5)^2