Координаты точки пересечения (-1; 3)
Решение системы уравнений х= -1
у=3
Объяснение:
Решите графически систему уравнений у+3х=0 и у-3х=6
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде нужно преобразовать уравнения в более удобный для вычислений вид:
у+3х=0 у-3х=6
у= -3х у=6+3х
Таблицы:
х -1 0 1 х -1 0 1
у 3 0 -3 у 3 6 9
Согласно графику, координаты точки пересечения (-1; 3)
Решение системы уравнений х= -1
у=3
1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
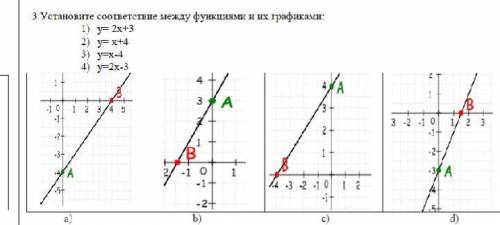
1) 14·x-12·y+14=0
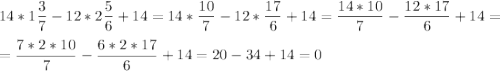
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
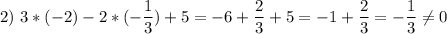
не является решением
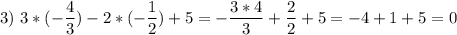
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
В решении.
Объяснение:
3. Установите соответствие между функциями и их графиками:
1) y= 2x+3
2) y=x+4
3)y=x-4
4) y=2х-3
Применить уравнение линейной функции у = kx + b:
а) Установить координаты точек: А(0; -4); В(4; 0);
Составить систему уравнений, используя координаты точек:
у = kx + b;
-4 = k * 0 + b
0 = k * 4 + b
Из первого уравнения b = -4, подставить во второе уравнение, вычислить k:
0 = 4k - 4
-4k = -4
k = -4/-4
k = 1;
Уравнение функции: у = х - 4; 3);
b) Установить координаты точек: А(0; 3); В(-1,5; 0);
Составить систему уравнений, используя координаты точек:
у = kx + b;
3 = k * 0 + b
0 = k * (-1,5) + b
Из первого уравнения b = 3, подставить во второе уравнение, вычислить k:
0 = -1,5k + 3
1,5k = 3
k = 3/1,5
k = 2;
Уравнение функции: у = 2х + 3; 1);
с) Установить координаты точек: А(0; 4); В(-4; 0);
Составить систему уравнений, используя координаты точек:
у = kx + b;
4 = k * 0 + b
0 = k * (-4) + b
Из первого уравнения b = 4, подставить во второе уравнение, вычислить k:
0 = -4k + 4
4k = 4
k = 4/4
k = 1;
Уравнение функции: у = х + 4; 2);
d) Установить координаты точек: А(0; -3); В(1,5; 0);
Составить систему уравнений, используя координаты точек:
у = kx + b;
-3 = k * 0 + b
0 = k * 1,5 + b
Из первого уравнения b = -3, подставить во второе уравнение, вычислить k:
0 = 1,5k - 3
-1,5k = -3
k = -3/-1,5
k = 2;
Уравнение функции: у = 2х - 3; 4).