ответ:
d=b^2-4ac=(-1)^2-4*1*(-72)=1+288=\sqrt{289}
289
=17
х1=\frac{-b- \sqrt{d} }{2a} = \frac{1-17}{2} = \frac{-16}{2} =-8
2a
−b−
d
=
2
1−17
=
2
−16
=−8
х2=\frac{-b+ \sqrt{d} }{2a} = \frac{1+17}{2} = \frac{18}{2} = 9
2a
−b+
d
=
2
1+17
=
2
18
=9
ответ: -8 и 9
d=b^2-4ac=7^2-4*(-4)*(-3)=49-48=\sqrt{1} =1
1
=1
х1=\frac{-b- \sqrt{d} }{2a} = \frac{-7-1}{2*(-4)} = \frac{-8}{-8} =1
2a
−b−
d
=
2∗(−4)
−7−1
=
−8
−8
=1
х2=\frac{-b+ \sqrt{d} }{2a} = \frac{-7+1}{(-8)} = \frac{-6}{-8} =0,75
2a
−b+
d
=
(−8)
−7+1
=
−8
−6
=0,75
По формуле:
Зная это получаем:
Известно что:
отсюда получаем:
Получаем 2 уравнения:
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
Теперь надо найти при каких значениях k и n решения лежат на отрезке![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1)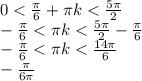
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
Поскольку n принадлежит целым числам, то получается что n=0,1