По формуле классической вероятности: p=m/n n=90 ( количество двузначных чисел)
Числа делящиеся на 3: 12; 15;... 99 - таких чисел 30 Можно найти их количество по формуле n-го члена арифметической прогрессии a₁=12 d=15-12=3 99=12+3·(n-1) ⇒87=3(n-1) n-1=29 n=30
Числа делящиеся на 5: 10; 15;20; 25; 30;...; 95 - таких чисел 30 Можно найти их количество по формуле n-го члена арифметической прогрессии a₁=10 d=15-10=5 95=10+5·(n-1) ⇒85=5(n-1) n-1=19 n=20
Чисел, которые одновременно делятся и на 3 и на 5 всего 6: 15;30;45;60;75 и 90
Сначала определим время, за которое мотоциклист планировал проехать свой путь (первоначальная скорость=Х). t=120:X Потом он ехал со скоростью 1,2 Х те же 120 км, плюс остановка в пути 15 минут, это 0,25 часа (15:60=0,25). Можем составить уравнение: 120:Х =120:1,2Х + 0,25 Приводим к общему знаменателю, это 1,2Х , подписываем дополнительные множители, перемножаем и получаем новое уравнение: 144 = 120 + 0,3Х -0,3Х = 120 - 144 -0,3Х = - 24 0,3Х = 24 Х = 24 : 0,3 Х = 80 (км\час, первоначальная скорость мотоциклиста). ПРОВЕРКА: 120:80=1,5 (часа) 120:96+0,25=1,5(часа).
1) 45000 = 4,5*10⁴ порядок числа равен 4
2) 260 = 2,6*10² порядок числа равен 2
3) 0,00024 = 2,4*10⁻⁴ порядок числа равен -4
4) 0,032 = 3,2*10⁻² порядок числа равен -2
5) 0,059 * 10⁸ = 5,9*10⁻²*10⁸ = 5,9*10⁶ порядок числа равен 6
6) 526*10⁴ = 5,26*10²*10⁴=5,26*10⁶ порядок числа равен 6
Пояснение:
Стандартным видом числа а называют его запись в виде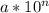 ,
,
где 1 < а < 10 и n — целое число. Число n называется порядком числа а.