Смотри решение.
Объяснение:
Найденный дискриминант обведен в рамочку на фотографии:
На всякий случай, даю полное решение данного уравнения, там и дискриминант уравнения, и его корни:
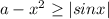
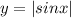расположен выше оси ОХ. 
.
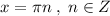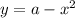- это параболы , ветви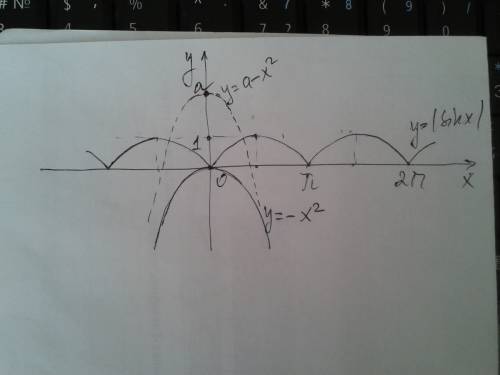
Дано уравнение: 3x² - 7x + 4 = 0. Нужно найти дискриминант данного уравнения.
Дискриминант квадратного уравнения вычисляется по формуле: D = b² - 4ac, где a -- коэффициент при x², b -- коэффициент при x, а c -- свободный член уравнения.
В данном случае: a = 3, b = -7, c = 4.
Подставим данные в формулу дискриминанта: D = (-7)² - 4 · 3 · 4 = 49 - 48 = 1.
ответ: D = 1.
*** На всякий случай добавлю решение уравнения:
x₁ = (7 - 1) / (2 · 3) = 6 / 6 = 1
x₂ = (7 + 1) / (2 · 3) = 8 / 6 = 4 / 3 ***