Координаты точки пересечения можно найти методом вычитания:
а) чтобы найти переменную , достаточно вычесть от верхней части системы нижнюю, тогда получится , найдем координату , подставим значение х в любую часть системы: , следовательно точка пересечения этих прямых будет находится по координатам
б) , искомый ответ будет
в) тут возникает противоречие, если прямые вычесть, то мы не сможем найти или , или же будет , что не является верным, значит прямые не будут пересекаться, они являются параллельными
г) тут уже можно сразу найти , искомый ответ будет
ответ: а), б), в)Нет решения, г)
Примечание: Если в г была система такая , то это это две прямые, которые совпадают и ответом будет бесконечное множество.
Пусть мы имеем неравенство с двумя переменными одного из следующих видов:y > f(x); y ≥ f(x); y < f(x); y ≤ f(x).Для изображения множества решений такого неравенства на координатной плоскости поступают следующим образом:1. Строим график функции y = f(x), который разбивает плоскость на две области.2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией. ну вообще это основное, а там уже смотри по заданию как))
Объяснение:
Координаты точки пересечения можно найти методом вычитания:
а)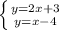
чтобы найти переменную 
, достаточно вычесть от верхней части системы нижнюю, тогда получится 
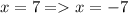, найдем координату 
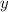, подставим значение х в любую часть системы: 
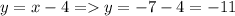, следовательно точка пересечения этих прямых будет находится по координатам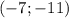 
б)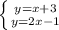
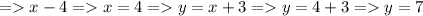, искомый ответ будет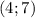 
в)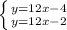
тут возникает противоречие, если прямые вычесть, то мы не сможем найти 
или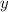 
, или же будет 
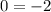, что не является верным, значит прямые не будут пересекаться, они являются параллельными
г)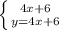
тут уже можно сразу найти 
, искомый ответ будет 
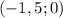
ответ: а)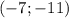
, б)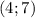
, в)Нет решения, г)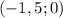
Примечание: Если в г была система такая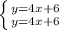
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.