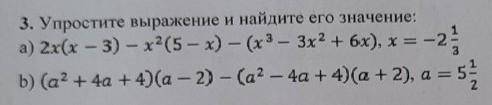
Пусть первая бригада, работая отдельно, может убрать урожай за x дней, а вторая - за y дней. Тогда за 1 день первая бригада выполнит 1/ x часть работы, а вторая - 1/y. Работая совместно, за 1 день они уберут (1/x + 1/y) часть урожая, которая по условию задачи равна 1/12. Таким образом,ВЛОЖЕНИЕ №1.
Далее, за восемь дней совместной работы две бригады уберут 8(1/x + 1/y) часть урожая, а за последующие семь дней вторая бригада выполнит 7/y часть работы. В результате будет выполнена вся работа. Следовательно,ВЛОЖЕНИЕ №2.
Чтобы решить систему уравнений (2)-(3) подставим из уравнения ВЛОЖЕНИЕ №4. Мы получим ВЛОЖЕНИЕ №3.
откуда У=21. Тогда Х=28 . Таким образом, первая бригада, работая отдельно, могла бы убрать урожай за 28 дней.
ответ: 28
a) 2x(x-3)-x²(5-x)-(x³-3x²+6x)=2x²-6x-5x²+x³-x³+3x²-6x=2x²-12x-5x²+3x²=-12x= -12×(-2 ⅓)= -12/1×(-7/3)=28
Объяснение: x³ и -x³ сократились так как это противоположные числа; 2x²-5x²+3x²=0 и поэтому остаётся -12x; / ←эта палочка является у меня дробной чертой
b) (a²+4a+4)(a-2)-(a²-4a+4)(a+2)=(a-2)(a²+4a+4)-(a+2)(a²-4a+4)=(a³-2³)-(a³+2³)=a³-8-a³-8=-16