
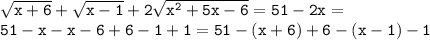
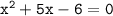 :
: 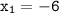 ,
, 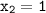
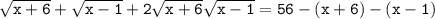
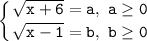 , тогда
, тогда 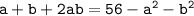
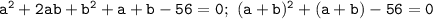
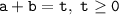 (ведь выражения
(ведь выражения  и
и 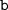 неотрицательны) и по теореме, обратной теореме Виета, найдём корни уравнения
неотрицательны) и по теореме, обратной теореме Виета, найдём корни уравнения 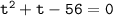 :
: 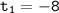 (не удовлетворяет ограничениям, приведённым выше),
(не удовлетворяет ограничениям, приведённым выше), 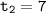
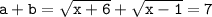 ; решим уравнение, возведя обе части в квадрат (делать это можно постольку, поскольку обе части уравнения неотрицательны):
; решим уравнение, возведя обе части в квадрат (делать это можно постольку, поскольку обе части уравнения неотрицательны): 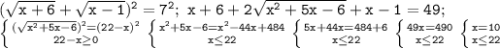

вот этот вариант за рания мне за что