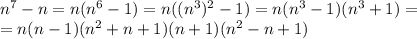 . Так как среди любых трех последовательных целых чисел по крайней мере одно делится на 2 и одно на 3, то при любых целых n число
. Так как среди любых трех последовательных целых чисел по крайней мере одно делится на 2 и одно на 3, то при любых целых n число  делится на
делится на 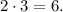 Следовательно, число
Следовательно, число 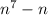 делится на 6, если n - любое число.
делится на 6, если n - любое число.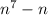 делится на 7, если n - натуральное число. Для начала исследуем методом математической индукции
делится на 7, если n - натуральное число. Для начала исследуем методом математической индукции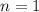 имеем
имеем 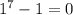 - кратное 7.
- кратное 7.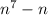 делится на 7 при каком-нибудь произвольном натуральном
делится на 7 при каком-нибудь произвольном натуральном 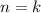 , т.е.
, т.е. 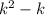 кратно 7.
кратно 7.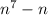 делится на 7 и при
делится на 7 и при 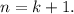
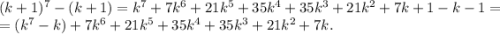
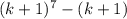 картно 7, если n - натуральное число.
картно 7, если n - натуральное число.
K2O оксид калия |
СаО оксид кальция ||
MnO оксид марганца ||
Fe2O3 оксид железа |||
V2O5 оксид ванадия V
Li2O оксид лития |
Bi2O3 оксид висмута |||
Cr2O3 оксид хрома |||
MgO оксид магния ||
Al2O3 оксид алюминия |||
Неметаллы:
SO3 оксид серы VI
As2O3 оксид мышьяка |||
Cl2O7 оксид хлора Vll
SiO2 оксид кремния |V
P2O5 оксид фосфора V
N2O3 оксид азота |||
B2O3 оксид бора |||
СО оксид углерода ||
SeO2 оксид селена IV
I2O5 оксид йода V
Оксиды солей ???:
KClO3 хлорат калия
NaClO гипохлорит натрия