 ;
;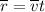 ;
;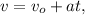 либо в векторном виде:
либо в векторном виде: 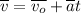 ;
;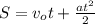 либо в векторном виде:
либо в векторном виде: 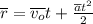 ;
;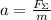 либо в векторном виде:
либо в векторном виде: 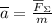 ;
; ;
;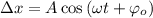 ;
;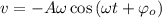 ;
; ;
;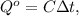 где
где 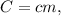 либо в удельном виде:
либо в удельном виде:  ;
;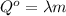 ;
;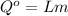 ;
; ;
; ;
;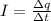 ;
;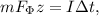 где
где  ;
;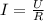 ;
;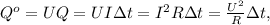
 ;
;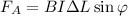 ;
; ;
;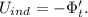
Примечание: в скобках пишу менее вероятные ответы .
1. 7 ( 8 c учетом варианта , что никто не вышел из лифта)
2. 330 ( 660 с учетом порядка выхода , 6 без учета этажей , 12 без учета этажей , но с учетом порядка выхода)
3. 990
4. 1331 ( 1716 - c учетом порядка выхода)
А что верно на самом деле , тут уже вопрос не ко мне , а к бестолковым составителям этого задания.
Объяснение:
1. пассажиры могут выйти на одном и том же этаже (порядок выхода не имеет значения);
Пусть в лифте будет только 1 пассажир . Он может выйти либо не выйти из лифта . То есть 2 варианта . Пусть будет 2 пассажира в лифте . Поскольку второй тоже может выйти , а может не выйти , то общее число вариантов 2*2= 4 . Аналогично для 3 пассажиров ,число вариантов : 4*2 =2^3 = 8. Примечание : для n человек в лифте , число равно :N= 2^n.
Но тут есть непонятный момент в условии. Возможен ли такой вариант , что все пассажиры не вышли из лифта? Если возможен , то ответ 8 , а вот если невозможен ,то ответ 7. Как всегда авторы забыли прояснить главное.
2. два человека могут выйти на одном этаже, а третий – на другом;
Найдем сначала общее число пассажирам выйти на двух этажах из 11 ( на первом этаже выйти не могут).
Это число равно : C (11 ,2)=11!/(2!*9!) =10*11/2=55 - сочетания из 11 этажей по два этажа.
В каждом из выхода людей по этажам , на первом из них может выйти какие-то два человека , а на втором третий оставшийся.
Или наоборот на первом может выйти один человек , а на втором два оставшихся. Таким образом ,общее число
2*C(3,2) = 2*3!/(2!*1!) = 6
Тогда общее число вариантов :
N = 6*55 =330
Но опять же неясно , что имели ввиду авторы. Нужно ли учитывать на каком этаже выходят люди? Если да , то ответ 330. Если же люди должны выходить на фиксированных этажах , то ответ : 6.
Более того , я так и не понял важен ли порядок выхода на
этажах во втором задании? Если важен , то нужно еще умножить на 2.
То ответ будет: 660.
3. люди могут выйти на разных этажах;
Поскольку все люди должны выйти на разных этажах , то на каждом этаже может выйти только по одному человеку.
Общее число выбрать 3 этажа для выхода равно :
C (11,3) = 11!/(3!*8!) = 9*10*11/(2*3) = 3*5*11= 55*3=165
Общее число как пассажиры могут выйти на этих 3 этажах равно : 3! =6.
Тогда число равно : 6*165 = 990
4. пассажиры могут выйти из лифта
Тут нужно рассмотреть все варианты.
Если на одном этаже выходит по одному человеку , то число вариантов : N1 =990.
Если на одном выходит два человека , а на другом третий оставшийся , то число вариантов : 330 - без учета порядка выхода и 660 - с учетом порядка выхода.
Осталось рассмотреть вариант , когда все 3 человека выходят на фиксированном этаже :
Без учета порядка выхода таких вариантов 11 , а с учетом порядка выхода : 3!*11 = 66.
Тогда общее число вариантов без учета порядка выхода :
990 +330 + 11 =1331
С учетом порядка выхода :
990 +660 +66 = 1716
Результат : 1331 можно получить другим
Определенный человек может выйти на 11 различных этажах . Всего у нас 3 человека , поэтому рассуждая как в первом задании , получаем , что общее число
N=11^3 = 1331 - это значит , что мы решили задачу правильно.
1)x^2+9x+14=0
3)x^2-10x/3+8/3=0
5)x^2-8/7+16/49=0
7)x^2-(V2+V5)x+V10=0
9)x^2-(V2-V7)x-V14=0