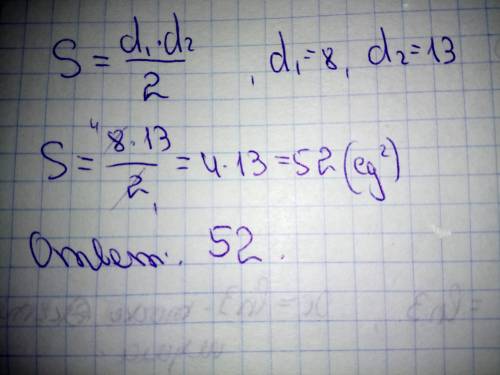
Реши задачу и запиши ответ Диагонали ромба равны 8 и 13. Найди площадь этого ромба.

Question

Алгебра: Реши задачу и запиши ответ Диагонали ромба равны 8 и 13. Найди площадь этого ромба.

hcufiyicii · Accepted Answer

Значения высоты, на которую отскакивает шар, составляют убывающую геометрическую прогрессию с 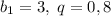$b_1=3,\;q=0,8$ .

Сумма вертикальных расстояний, пройденных мячом вниз - это сумма всех членов убывающей прогрессии

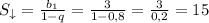$S_{\downarrow}=\frac{b_1}{1-q}=\frac3{1-0,8}=\frac3{0,2}=15$ метров.

Сумма вертикальных расстояний, пройденных мячом вверх - это сумма всех членов убывающей прогрессии за вычетом первого члена (т.к. на 3 м вниз мяч пролете только вниз)

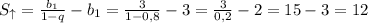$S_{\uparrow}=\frac{b_1}{1-q}-b_1=\frac3{1-0,8}-3=\frac3{0,2}-2=15-3=12$ м.

Тогда сумма вертикальных расстояний пройденных мячом вниз и вверх

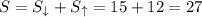$S=S_{\downarrow}+S_{\uparrow}=15+12=27$ метров метров.

P.S. Можно рассмотреть расстояния, пройденные вниз как г.п. с 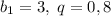$b_1=3,\;q=0,8$ , а расстояния, пройденные вверх как г.п. с 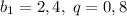$b_1=2,4,\;q=0,8$ и найти сумму каждой г.п. ответ будет тем же.

MOGZ ответил