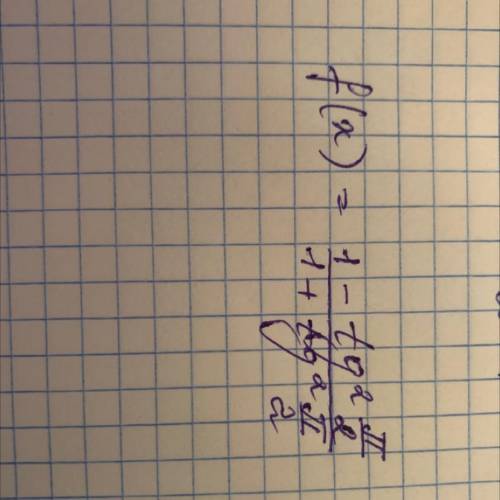
Дана арифметическая прогрессия:
а1, а2, а3, а4, а5, а6, а7, а8, а9, а10, а11, а12, а13, а14, а15, а16, а17, а18, а19, а20 ...
где аn = а1 + (n - 1)х
х - некое произвольное число, которое прибавляется к каждому следующему члену прогрессии.
Известно, что:
а7 + а8 + а9 + а10 + а11 + а12 = 4
Нужно найти:
а1 + а2 + а3 + а4 + а5 + а6 + а7 + а8 + а9 + а10 + а11 + а12 + а13 + а14 + а15 + а16 + а17 + а18 = ?
Решение:
а7 + а8 + а9 + а10 + а11 + а12 = а1 + 6х + а1 + 7х + а1 + 8х + а1 + 9х + а1 + 10 х + а1 + 11х = 6 а1 + 51х
6 а1 + 51х = 4
а1 + а2 + а3 + а4 + а5 + а6 + а7 + а8 + а9 + а10 + а11 + а12 + а13 + а14 + а15 + а16 + а17 + а18 = 18 а1 + (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17)х = 18 а1 + 153х = 3 (6 а1 + 51х) = 3 * 4 = 12
ответ: 12
д) (u+v)(u-v)(u-v)
е) (u +v)(u^2 -uv+v^2)(u+v)
2) а) 1/х1 +1/х2 = (х2 +х1)/х1*х2 по теореме Виета х2+х1= -1/6 х1*х2 = -2/6, значит
1/х1 +1/х2 = (-1/6): (-2/6)= 1/2=0,5
в) (х1^3 +x2 ^3)/(x1 ^3 * x2^3) = (x1+x2)(x1^2 -x1*x2 +x2^2)/(x1*x2)^3 = (x1+x2)(x1^2 -x1*x2 +x2^2 -2x1*x2+2x1*x2)/(x1*x2)^3 = (x1+x2)((x1 +x2)^2 -3x1x2)/(x1*x2)^3 = -1/6 * (1/36 +2/3)/ (-8/216) = -1/6 *25/36 /(-8/216) = -25/216 *(-216/8) = 25/8
б) (-1/6)^2 - 2* (-2/6))^2 - 2*(-2/6)^2 = (1/36 +4/6)^2 - 4/18 = 625/1296 - 4/18 =337/1296