Б) f(x)=4-2x f`(x)=(4-2x)`=(4)`-(2x)`=0-2·(x)`=-2·1=-2 Применили правила: производная суммы( разности) равна сумме( разности) производных Производная постоянной (C)`=0 Постоянный множитель можно вынести за знак производной (х)`=1 Производная принимает во всех точках одно и то же значение (-2) f`(0,5)=f`(-3)=-2
в) f(x)=3x-2 f`(x)=(3x-2)`=(3х)`-(2)`=3·(x)`-0=3·1=3 Применили правила: производная суммы( разности) равна сумме( разности) производных Производная постоянной (C)`=0 Постоянный множитель можно вынести за знак производной (х)`=1 Производная принимает во всех точках одно и то же значение (3) f`(5)=f`(-2)=3
Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию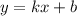
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.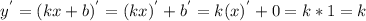
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.