5. Расстояние между пунктами А и Б равно 1 км. Андрей вышел из пункта А по направлению к пункту Б. Одновременно с ним из пункта Б в том же направ-
лении вышел Борис со скоростью на 0,5 км/ч меньше скорости Андрея, удаля-
ясь от пункта А. Их встреча произошла на расстоянии 8 км от пункта Б. Каким
было расстояние между Андреем и Борисом, когда Андрей дошел до пункта Б?
6. Расстояние между пунктами А и Б равно 12 км. Первый и второй велоси-
педист выехали из пункта А в пункт Б, и в то же время навстречу из пункта Б
выехал третий велосипедист, который после выезда через 18 мин встретился с
первым велосипедистом, а еще через 2 мин после этого встретился со вторым
велосипедистом. На сколько скорость первого велосипедиста больше скорости
второго велосипедиста?
7. Два катера имеют одинаковую собственную скорость движения. Первый
катер поплыл из пункта А по течению в направлении пункта Б. Одновременно
из пункта Б навстречу поплыл другой катер и встретился с первым катером, ко-
гда первый катер проплыл 5
8
расстояния между пунктами А и Б. Во сколько раз
собственная скорость катеров больше скорости течения реки?
8*. По берегу реки в направлении течения последовательно расположены
пристани А, Б, В так, что расстояния от А до Б и от Б до В равны 15 км. На мо-
торной лодке путь от Б до В и затем от В до А занимает 1 ч 25 мин, а путь от Б
до А и затем от А до Б занимает 1 ч 20 мин. Найдите скорость течения реки.
9. По улицам города водитель треть пути ехал со скоростью 40 км/ч, еще чет-
верть пути со скоростью 60 км/ч, а оставшуюся третью часть пути с такой по-
стоянной скоростью, что средняя скорость его движения на всем пути была
48 км/ч. С какой скоростью водитель проехал третью часть пути?
10. Два велосипедиста выехали с места старта по кольцевому маршруту од-
новременно в противоположных направлениях. Первому велосипедисту, кото-
рый ехал быстрее второго, после первой встречи нужно было ехать 1,8 км до
места старта, а второму велосипедисту после второй встречи нужно было ехать
0,4 км до места старта. Найдите длину кольцевого маршрута.
3
11*. Два спортсмена выбегают одновременно с места старта в одном направ-
лении по дорожке стадиона длиной 400 м со скоростями 16,8 и 17 км/ч. Сколько
метров до места старта придется бежать более быстрому спортсмену, когда рас-
стояние между спортсменами первый раз станет равным 20 м?
12. Водитель хотел проехать весь путь с одной скоростью за некоторое вре-
мя. Однако, передумал и часть пути проехал со скоростью на 20 % больше, чем
собирался ехать, а остальную часть пути со скоростью на 20 % меньше, чем со-
бирался в самом начале. В итоге получилось, что на весь путь он затратил такое
же время, что и планировал в начале. Какую часть пути водитель проехал с
меньшей скоростью?
13. Коля ехал в поезде со скоростью 76 км/ч, а Толя ехал по встречному пу-
ти. Расстояние между Колей и Толей дважды было равно 16 км, сначала через
5 ч после начала поездки Коли, а затем через 5 ч 12 мин после начала этой по-
ездки. С какой скоростью ехал Толя?
14. Водитель собирался проехать от одного города до другого с некоторой
постоянной скоростью за некоторое время. Если эту скорость увеличить на
20 %, то на весь путь ушло бы на полчаса меньше времени. А если скорость
уменьшить на 10 км/ч, то на весь путь ушло бы на 3
8
ч больше времени, чем
предполагалось. Найдите расстояние между городами.

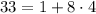 , поэтому
, поэтому 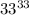 оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 3.
, то есть на 3. 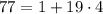 , поэтому
, поэтому  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 7. Значит, сумма
, то есть на 7. Значит, сумма  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и 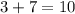 , то есть на 0. Искомый остаток равен нулю.
, то есть на 0. Искомый остаток равен нулю.
Найдём точку смены знака модуля: 2x + 4 = 0, x = -2
Получается, что на отрезке [-3;-2] функция убывает, а на отрезке [-2;3] функция возрастает. Причем возрастает симметрично относительно прямой x = -2, поэтому в точке x = 3 будет наибольшее значение функции.
f(3) = 9.
Наибольшее значение функции = 9.
Так как минимальное значение функции y = |2x+4| - это 0, то отнимая от функции 1, получаем, что минимальное значение = -1.
9 - (-1) = 10
ответ: 10