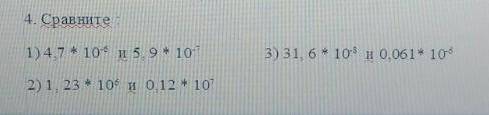
1,4-(кор)2
<0
(1+2x)( x-3)
1,4-(кор)2 меньше нуля, т.к. кор2 больше, чем 1,4. Следовательно, знаменатель дроби должен быть больше нуля. Решаем неравенство (1+2х)(х-3) больше нуля 2(1/2+х)(х-3) больше нуля На числовой прямой обозначаем две пустые точки -1/2 и 3 Считаем знаки в полученных интервалах. Получаем слева направо "+", "-", "+". Нам нужны те интервалы, в которых плюс, т.к. функция должна быть больше нуля. Итак, х принадлежит объединению интервалов от минус бесконечности до -1/2 открытому с интервалом от 3 до плюс бесконечности открытому.Пусть первый рабочий выполняет работу за х часов,тогда второй- за х+4.
кол-во деталей в час первого пусть будет y,тогда у второго это y-4.
Составляем систему уравнений и решаем ее --> x*y=165
и (x+4)(y-4)=165.
Выражаем из первого х или y и подставляем во второе уравнение.Решаем уравнение с одним неизвестным.Находим его.
х=165/y.
(165/y + 4)(y-4)=165
165y+4y^2-16y-660=165y
4y^2-16y-660=0 Сокращаем на 4 и решаем квадратное уравнение.
D=(-4)^2+ 4*165=676=(26)^2
Тогда y=(4+26)/2=15.Второй корень уравнение не подходит,т.к. он отрицательный.
ответ:15 деталей в час.
В решении.
Объяснение:
Сравнить:
1) 4,7*10^-6 и 5,9*10^-7;
4,7*10⁻⁶ и 5,9*10⁻⁷;
1/4,7⁶ и 1/5,9⁷;
1/4,7⁶ > 1/5,9⁷;
Чем больше знаменатель, тем меньше значение дроби.
2) 1,23*10^6 и 0,12*10^7;
1,23*10⁶ и 0,12*10⁷;
Привести второе число к стандартному виду:
1,23*10⁶ и 1,2*10⁶;
1,23*10⁶ > 1,2*10⁶;
Если показатели степени одинаковые, больше то число, основание которого больше.
3) 31,6*10^-8 и 0,061*10^-8;
31,6*10⁻⁸ и 0,061*10⁻⁸;
1/31,6⁸ и 1/0,061⁸;
Привести оба знаменателя к стандартному виду:
1/3,16⁹ и 1/6,1⁶;
1/3,16⁹ < 1/6,1⁶;
Чем больше знаменатель, тем меньше значение дроби.