Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : .
Сумма арифметической прогрессии считается по формуле где a1 - первый член прогресси; d - шаг или разность прогрессии; n - количество членов, которые надо просуммировать. (Кстати, это одна из формул для суммы первых n членов)
Первый член у нас задан, он равен a1= -9, количество первых членов n=5. Задан и шаг, только необычно. В арифметической прогрессии каждый член, кроме первого, отличается на одну и ту же величину (шаг). Нам задано, что (n+1)-й член меньше n-го члена на 16. Это означает, что шаг равен d = -16. С минусом, т.к. каждый последующий член меньше:
1) Решение через дискриминант .
2) Решение с выделения полного квадрата .
3) Решение с теоремы Виета.
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
.
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :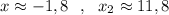 .
.