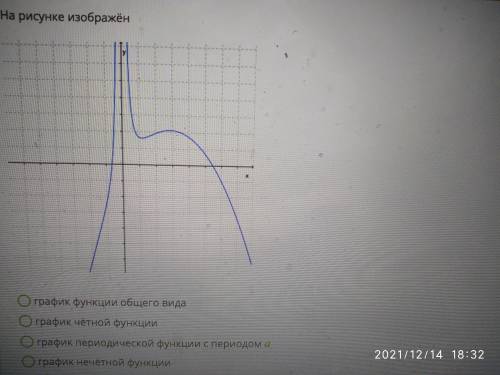
1. Это неполные квадратные уравнения (для стандартного вида не хватает свободного члена С).
Все уравнения такого типа решаются примерно одинаково.
Общий множетель - Х. Нужно вынести его за скобки.
Получаем: Х(1-3Х)=0. Надо знать, что уравнение равно 0, если один из множетелей равен 0. То есть Х=0 ИЛИ 1-3Х=0
-3Х=-1
3Х=1
Х=1/3
2.
Упростим и получим: -25х^2=-36
Возможные корни этого уравнения: x=-6/5, x=6/5
Подробно смотри вложения.
3. Смотри вложения.
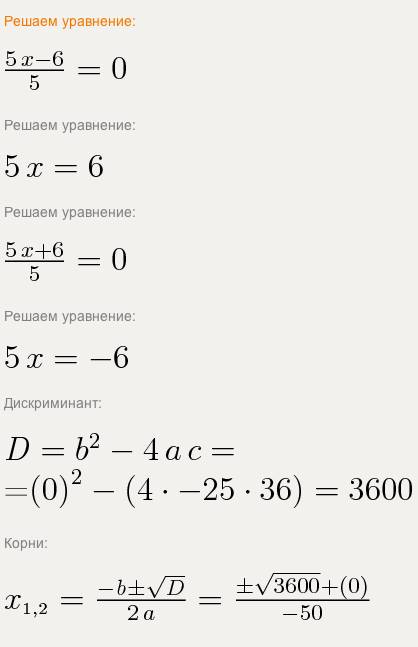
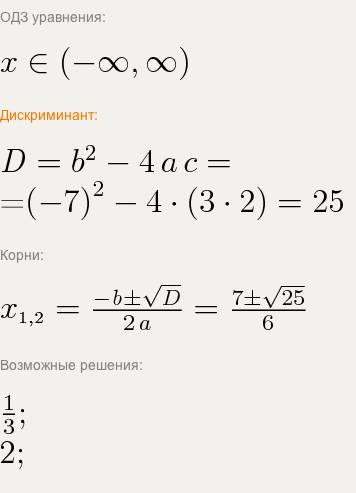
Первый проще взять по частям, нафиг тут подстановка.
u = x du = dx;
dv = cos³xdx v = ∫cos²x d(sinx) = ∫1-sin²xd(sinx) = sinx - sin³x/3;
∫ = uv - ∫vdu = x[sinx - sin³x/3] - ∫sinx - sin³x/3 dx.
Вычисляем второй интеграл.
∫sinx dx = -cosx;
∫sin³x/3 dx = -(1/3)∫sin²x d(cosx) = -(1/3)∫1-cos²xd(cosx) = -(1/3) [cosx - cos³x/3]
Все, дальше думай головой :))
А второй - да, проще подставить. lnx = t x=e^t; dx = e^tdt
∫t*e^tdt - а теперь по частям по той же схеме. Получится x*lnx - x
Константы везде выкинул, но не забывай о них ))