Question

Сколько решений имеет система уравнений
{

$|x - y | = 1$
$xy = - 2$

Answer 1

(см. объяснение)

Объяснение:

Рассмотрим первую строку системы:

$|x-y|=1$

Поскольку и левая, и правая части уравнения неотрицательны, то возведение в квадрат даст равносильное равенство:

$x^2-2xy+y^2=1$

Из второй строки системы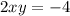 $2xy=-4$.

Тогда:

$x^2+4+y^2=1\\x^2+y^2=-3$

Это равенство неверно.

Тогда система имеет 0 решений.

Задание выполнено!

(В прикрепленном файле показано менее изящное решение)