1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
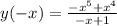
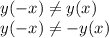
Это функция общего вида
2)
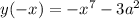
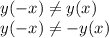
Это функция общего вида
3)
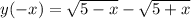
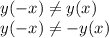
Это функция общего вида
3.
1)
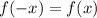
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/3904/3705/69e2d.png)
2)
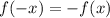
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/3904/3705/5cc0f.png)
4.
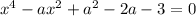
Это биквадратное уравнение. Делаем подстановку
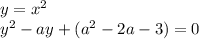
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
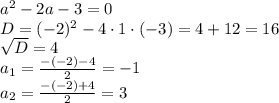
Делаем проверку:
1) а=-1
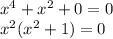
Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
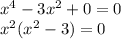
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
1)
{
x
+
2
y
=
0
,
5
x
+
y
=
−
18
;
2)
{
2
x
−
5
y
=
10
,
4
x
−
y
=
2
;
3)
{
x
−
2
y
=
1
,
y
−
x
=
−
2
;
4)
{
x
+
y
=
−
3
,
x
−
y
=
−
1.
Решение 1
{
x
+
2
y
=
0
,
5
x
+
y
=
−
18
;
x + 2y = 0
x = −2y
Решение рисунок 1
5x + y = −18
y = −18 − 5x
Решение рисунок 2
Решение рисунок 3
Графики уравнений пересекаются в точке (−4;2), следовательно данная пара чисел является решением данной системы уравнения.
Решение 2
{
2
x
−
5
y
=
10
,
4
x
−
y
=
2
;
2x − 5y = 10
−5y = 10 − 2x
y
=
2
5
x
−
2
Решение рисунок 1
4x − y = 2
−y = 2 − 4x
y = 4x − 2
Решение рисунок 2
Решение рисунок 3
Графики уравнений пересекаются в точке (0;−2), следовательно данная пара чисел является решением данной системы уравнения.
Решение 3
{
x
−
2
y
=
1
,
y
−
x
=
−
2
;
x − 2y = 1
x = 1 + 2y
Решение рисунок 1
y − x = −2
y = x − 2
Решение рисунок 2
Решение рисунок 3
Графики уравнений пересекаются в точке (3;1), следовательно данная пара чисел является решением данной системы уравнения.
Решение 4
{
x
+
y
=
−
3
,
x
−
y
=
−
1.
x + y = −3
y = −3 − x
x − y = −1
−y = −1 − x
y = x + 1
Графики уравнений пересекаются в точке (−2;−1), следовательно данная пара чисел является решением данной системы уравнения.
Объяснение:
Оценка - на усмотрение учителя. Четких правил нет.
Каждое задание "стоит" определенное количество балов. Главное в работе - набрать необходимое количество балов (например, можно решить ПРАВИЛЬНО 2 последних задания и заработать 7- или ПРАВИЛЬНО решить 2 первых задания и заработать всего ).