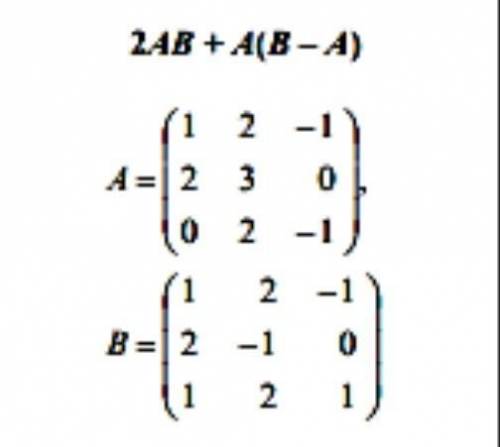
1) -6x - 5 = 4x
-6x - 4x = 5
-10x = 5
x = 5 : (-10)
x = -0,5
2) -5x = 5x - 6
-5x - 5x = -6
-10x = -6
x = -6 : (-10)
x = 0,6
3) 2 + 8x = 3x + 9
8x - 3x = 9 - 2
5x = 7
x = 7 : 5
x = 1,4
4) 5 - 2x = 8x + 9
-2x - 8x = 9 - 5
-10x = 4
x = 4 : (-10)
x = -0,4
5) x - x/7 = -9/14 |*14
14x - 2x = -9
12x = -9
x = -9 : 12
x = -0,75
6) x - x/9 = -26/9 |*9
9x - x = -26
8x = -26
x = -26 : 8
x = -3,25
7) x + x/2 = -12 |*2
2x + x = -24
3x = -24
x = -24 : 3
x = -8
8) x + x/12 = -13/4 |*12
12x + x = -39
13x = -39
x = -39 : 13
x = -3
9) x + x/2 = 9/2 |*2
2x + x = 9
3x = 9
x = 9 : 3
x = 3
10) x/5 + x/9 = -14/15 |*45
9x + 5x = -42
14x = -42
x = -42 : 14
x = -3
11) 9 + x = x + 3/4
x - x = 3/4 - 9
0 = 3/4 - 9 -- неверно
корней нет
Объяснение:
Задача 1.
a1 = an - (n-1)*d = 59 - 3*n + 3 = 62 -3*n
Sn = (a1 + an)*(n/2) = 603
(62 - 3*n + 59)*n = 2*603 = 1206
(121 - 3*n)*n = 1206
- 3*n² + 121*n - 1206 = 0 a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 121² - 4*(-3)*(-1206) = 169 - дискриминант. √D = 13.
Вычисляем корни уравнения.
n = (-b+√D)/(2*a) = (-121+13)/(2*-3) = -108/-6 = 18 - первый корень
x₂ = (-b-√D)/(2*a) = (-121-13)/(2*-3) = -134/-6 = 22,33 - второй корень -нет
n = 18 - число членов - ответ.
а1 = an - (n-1)*d = 59 - 17*3 = 59 - 51 = 8 - а1 -первый член- ответ
Проверено - правильно.
Задача 2.
a1 = an - (n-1)*d = -8 + 5*n -5 = -13 +5*n
Sn = (-13 + 5*n - 8)*n = 30*2 = 60
5*n² - 11*n - 60 = 0 - НЕ РЕШЕНО.
ЗАДАЧА 3.
а1 = an - (n-1)*d = 49 - (n-1)*2 = 51 - 2*n
Sn = (a1 + an)*(n/2) = 702
(51 - 2*n + 49)*n = 702*2
- 2*n² + 100*n - 1404 = 0 - не решено.
Задача 4.
а1 = an - (n-1)*d = -18 + 7*n -7 = 7*n - 25
Sn = (a1 + an)*(n/2) =
(7*n - 25 -18)*n = -20*2 = -40
7*n² - 43*n + 40 = 0
D = b² - 4*a*c = -43² - 4*(7)*(40) = 729 - дискриминант. √D = 27.
Вычисляем корни уравнения.
n₁ = (-b+√D)/(2*a) = (43+27)/(2*7) = 70/14 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (43-27)/(2*7) = 16/14 = 1,14 - второй корень - нет
n = 5 - число членов - ответ
а1 = -18 - 4*(-7) = -18 + 28 = 10 - первый член
Проверено - правильно.
Можна підписку