y=-2x²+8x+13 (a=-2, b=8, c=13)
Координаты вершины параболы:
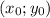
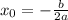
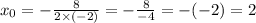
Подставляем ответ в функцию
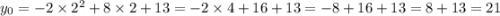
Координаты вершины параболы:
(2; 21)
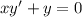
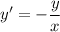 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными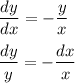
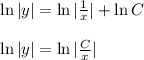
 - общее решение
- общее решение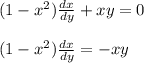

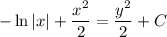 - общий интеграл
- общий интеграл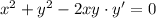

 , тогда
, тогда 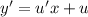



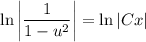
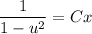
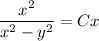 - общий интеграл
- общий интеграл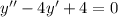
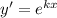 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
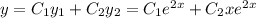 - общее решение
- общее решение
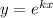 , тогда получаем
, тогда получаем
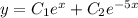

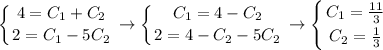
 - частное решение
- частное решение
x0=-b/2a=-8/(2*(-2))=2
y0=-2*4+16-13=-5
Или
y=-2(x^2-4x+4)-5
y=-2(x-2)^2-5
x-2=0
x=2
y=-5