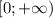![1)\ \ y=\sqrt{x^3-5x^2+6x}\\\\OOF:\ x^3-5x^2+6x\geq 0\ \ ,\ \ \ x(x^2-5x+6)\geq 0\ \ ,\ \ x(x-2)(x-3)\geq 0\ ,\\\\znaki:\ \ ---[\, 0\, ]+++[\ 2\ ]---[\ 3\ ]+++\\\\x\in [\ 0\ ;2\ ]\cup [\ 3;+\infty )\\\\\\2)\ \ \sqrt{6x-x^2}+\dfrac{1}{x-5}\\\\\\ODZ:\ \left\{\begin{array}{l}6x-x^2\geq 0\\x-5\ne 0\end{array}\right\ \ \left\{\begin{array}{l}x(6-x)\geq 0\\x\ne 5\end{array}\right\ \ \left\{\begin{array}{l}x\in [\ 0\ ;\ 6\ ]\\x\ne 5\end{array}\right](/tpl/images/2095/4522/cf5cb.png)
![x\in [\ 0\ ;\ 5\ )\cup (\ 5\ ;\ 6\ ]\\\\\star \ \ x\, (6-x)\geq 0\ \ ,\ \ x\, (x-6)\leq 0\ \ ,\ \ \ +++[\, 0\, ]---[\, 6\, ]+++\\\\x\in [\ 0\ ;\ 6\ ]\ \ \star](/tpl/images/2095/4522/325a7.png)
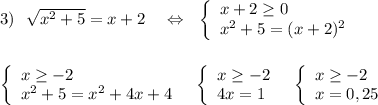
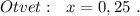
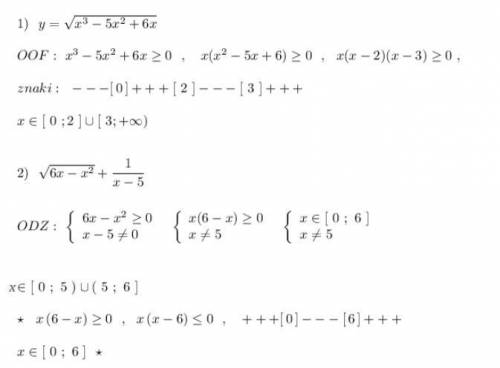
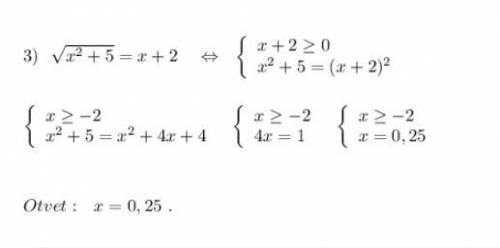
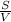 ,
,  = 4 часа — время, потраченное легковой машиной на путь.
= 4 часа — время, потраченное легковой машиной на путь. 
 квадратное неравенство вырождается в линейное
квадратное неравенство вырождается в линейное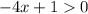
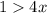
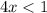
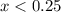
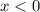
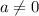

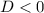 ) - отлично, график параболы выше оси Ох - неравенство выполняется
) - отлично, график параболы выше оси Ох - неравенство выполняется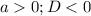
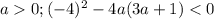

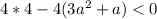
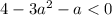
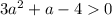
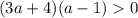
 авмтоматически
авмтоматически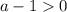 или
или 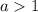
 -
- 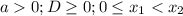 ;
; 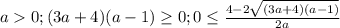
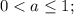 - с первых двух неравенств (аналогично по рассуждениям относительно первого случая)
- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)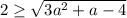
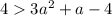
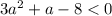 - что очевидно верно при условиях
- что очевидно верно при условиях