ответ: (2; 3)
Объяснение:
Решить графически уравнение:
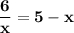
Построим два графика
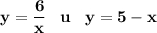
1.
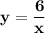
- функция обратной пропорциональности, график - гипербола.
Построим ветвь гиперболы:
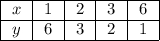
Вторую ветвь строим симметрично относительно начала координат.
2.
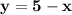
- линейная функция, график - прямая.
Для построения прямой достаточно двух точек:
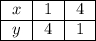
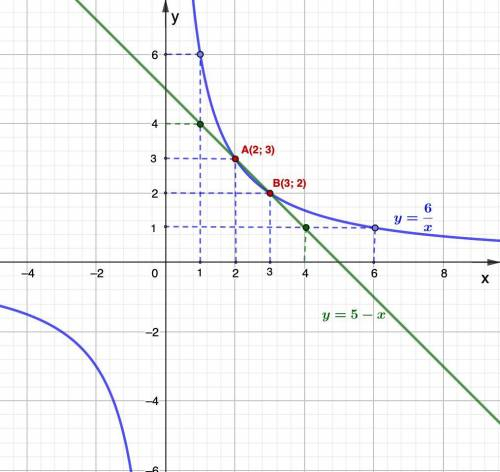
3. Построили графики.
Точки пересечения:
А (2; 3) и В (3; 2)
Решением уравнения будут абсциссы этих точек пересечения, то есть (2; 3).
Відповідь:
Пояснення:
г) 4/( x + 3 ) - 5/( 3 - x ) = 1/( x - 3 ) - 1 ; ОДЗ : x ≠ ± 3 ;
4/( x + 3 ) + 5/( x - 3 ) - 1/( x - 3 ) + 1 = 0 ;
4/( x + 3 ) + 4/( x - 3 ) + 1 = 0 ; │X ( x² - 9 ) ≠ 0
4( x - 3 ) + 4( x + 3 ) + ( x² - 9 ) = 0 ;
4x - 12 + 4x + 12 + x² - 9 = 0 ;
x² + 8x - 9 = 0 ;
x₁ = - 9 ; x₂ = 1 . - 9 i 1 Є ОДЗ .
В - дь : - 9 i 1 .
д) 3/x + 4/( x - 1 ) = ( 5 - x )/( x² - x ) ; ОДЗ : x ≠ 0 , x ≠ 1 ;
3/x + 4/( x - 1 ) - ( 5 - x )/[x( x - 1 ) ] = 0 ; │X x( x - 1 )
3( x - 1 ) + 4x - ( 5 - x ) = 0 ;
3x - 3 + 4x - 5 + x = 0 ;
8x - 8 = 0 ;
8x = 8 ;
x = 1 ; x = 1 ∉ ОДЗ .
В - дь : хЄ ∅ .
е) Аналогічно прикладу д) .
Надеюсь понятно написала