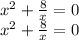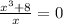
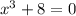
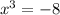
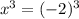
,х ≠ 0
, х ≠ 0
а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
Замена sinx=t
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
Возвращаемся к замене
sinx=1,5 sinx=-1\2
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
