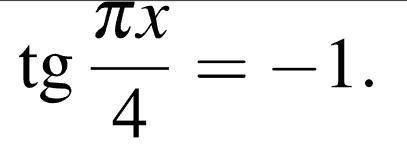
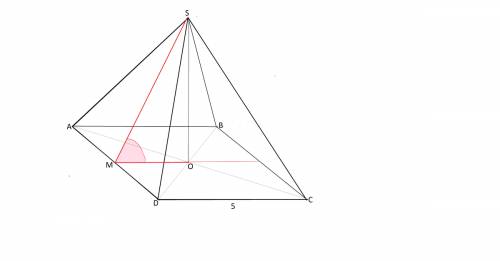
Сторона основания правильной четырехугольной пирамиды равна 5, а площадь ее полной поверхности равна 85. Найдите угол наклона боковой грани к плоскости основания.
-----------------------------------------------------
Сделаем рисунок пирамиды SABCD
Опустим высоту SO в центр основания, проведем апофему SM,
М соединим с О.
Для ответа на вопрос задачи нужно найти апофему SM ( проведем ее к стороне AD)
Ее найдем из площади боковой грани ( она для каждой грани одинакова,т.к. основание пирамиды - квадрат.
Сначала узнаем площадь боковой поверхности пирамиды, для чего из общей площади вычтем площадь основания.
Площадь основания - это площадь квадрата со стороной 5.
Sбок=85-5²=60
Площадь одной грани
S грани =60:4=15
Найдем апофему SM = h ASD
S ASD =AD*SM:2=5*SM:2
SM=15·2:5=6
cos SMO = МО:SM
МО= половина стороны основания и равна 2,5
cos ∠SMO=2,5:6
ответ:arсcos 2,5:6 (65° < угол < 66°)
----------------------
Если рисунок не открывается сразу, откройте его в новом окне или вкладке
Пусть время, за которое первая машина сделает копию всего пакета х мин.
Тогда вторая машина сделает копию всего пакета за х-30 мин.
Производительность первой машины 1/х.
Производительность второй машины 1/(х-30).
Если машины работают одновременно, то их производительность равна 1/20.
Составим и решим уравнение.
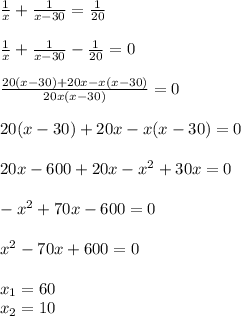
Первая машина выполнит всю работу за 60 мин. Вторая машина выполнит всю работу за 60-30 = 30 мин.
х₂=10 - посторонний корень, т.к. если бы первая машина выполняла всю работу за 10 мин, то вторая - за 10-30 = -20 мин. Это невозможно.
ответ: за 60 мин выполнит всю работу первая машина, за 30 мин выполнит всю работу вторая машина.
-1+4n, n∈Z
Объяснение:
tgβ= -1, если β=-π/4+πn, n∈Z (табличное значение)
В нашем случае, аргументом тангенса является угол πх/4, поэтому запишем решение так:
tg(πx/4) = -1
πx/4 = -π/4+πn, n∈Z
Теперь, обе части уравнения делим на π/4, получаем:
х = -π/4 : π/4 + πn/ (π/4), n∈Z
x = -1 + 4n, n∈Z