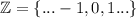
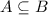 и
и 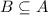
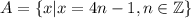
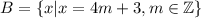


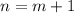
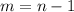
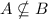 то,значит, есть такой элемент
то,значит, есть такой элемент 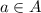 так что
так что 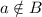 .
.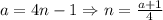
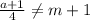
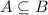
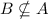 , то значит есть такой элемент
, то значит есть такой элемент 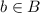 так что:
так что: 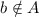
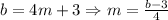
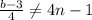
Раздел долго плана: Школа: Каскабулакская средняя школа
5.3C Множества ФИО учителя: Рашидов Махмуд Исмаилович
Дата: 28.07.2017г.
Класс: 5 Количество присутствующих:15 отсутствующих:
Тема урока
Объединение и пересечение множеств
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
5.4.1.2 знать определения объединения и пересечения множеств;
5.4.1.3 находить объединение и пересечение заданных множеств, записывать результаты, используя символы , ;
Цели урока
Дать определения объединения и пересечения множеств формированию навыков находить объединения и пересечение заданных множеств и записывают результаты используя символы , ;
Критерии успеха
Учащийся достиг цели обучения, если:
1. знает определения объединения и пересечения множеств
2. находит объединение и пересечение заданных множеств. 3.записывает результаты, используя символы , ;
Языковые цели
В ходе урока учащиеся будут оперировать новыми терминами и понятиями, комментировать порядок выполнения действий с множествами
Предметная лексика и терминология:
множества, пересечение и объединение; подмножества, пересекающиеся и непересекающиеся множества, пустое множество, элементы множества.
Точность и ясность словесного выражения мыслей.
Привитие ценностей
Воспитание чувства патриотизма. Формирование и поддержание доверительных межличностных отношений, взаимного уважения, взаимной ответственности. Воспитание цельной и порядочной личности, формирование у учащихся коммуникативных навыков и навыков лидера 21го века.
Межпредметные связи
Знания, полученные в данном разделе, найдут применение в алгебре, геометрии, биологии, истории.
Навыки использования ИКТ
Интерактивная доска, презентация ,интернет, мобильные устройства.
Предварительные
знания
Знает понятия множества и его элементов, пустого множества;
Определяет характер отношений между множествами (пересекающиеся и непересекающиеся множества);
Знаком с понятием подмножества;
Умеет использовать символы , , , , , при работе с множествами;
Ход урока
Запланированные этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
Оргмомент
Позитивный психологический настрой на урок
(3 мин)
Деление на группы с приема «Множества»
(5-мин)
Целеполагание
Постановка цели урока и определение критериев успеха и оценивания.
(5 мин)
Групповая работа
(3 мин)
Середина урока.
Презентация новой темы
(5мин)
Приветствует учеников, проверяет готовность к уроку, желает успеха.
Метод «Дерево достижений»
Педагог. Обратите внимание на наше одинокое дерево. У каждого из вас есть листочки разного цвета. Я по вас взять один из них (любого цвета) и нашему дереву покрыться разноцветной листвой.
Тех, кто выбрал зеленый лист, ожидает успех на сегодняшнем занятии.
Те, кто выбрал
Красный, — желают общаться.
Желтый — проявят активность.
Синий — будут настойчивы.
Помните, что красота дерева зависит от вас, ваших стремлений и ожиданий.
Деление на группы прием «Множества»
Ученики делятся на группы, выбирая разных животных – птицы, млекопитающие, насекомые.
Используя прием деления на группы, учитель наводит на тему урока, задавая наводящие во тем самым актуализирует знания учащихся о множествах.
Что такое множество?
Назовите элементы:
множества «Времена года»
множества «Дни недели»
Что такое подмножество?
Назовите подмножество:
Множества «Растения»
Множества «Спортсмены»
Цели уроки определяются с приема «Проблемная ситуация».
Введение в урок проблемного диалога необходимо для определения учащимися границ знания — незнания. Создание на уроке проблемной ситуации дает возможность учащемуся сформулировать цель занятия.
Учитель показывает ученикам задачу.
Махмуд и Екатерина содержат аквариумных рыбок. Махмуд коллекционирует только меченосцев, а Екатерина- рыбок красного цвета. У детей 8 меченосцев, а красных рыбок-7. Всего у детей-12 рыбок. Возможно ли такое?
Объяснение:
х=1... . . . . . .
Объяснение:
ответ х=1