Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
\[a{x^2} + bx = 0\]
Общий множитель x выносим за скобки:
\[x \cdot (ax + b) = 0\]
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
\[x = 0;ax + b = 0\]
Второе уравнение — линейное. Решаем его:
\[ax = - b\_\_\_\left| {:a} \right.\]
\[x = - \frac{b}{a}\]
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
\[1){x^2} + 18x = 0\]
Общий множитель x выносим за скобки:
\[x \cdot (x + 18) = 0\]
ДОЛЖНО БЫТЬ ПРАВИЛЬНО
Пусть скорость 1 бегуна = х км/ч .
Тогда скорость 2 бегуна = (х+11) км/ч .
За 1 час 1 бегун пробежал расстояние равное дуге АВ,
S(AB)=x*1 = x км .
А 2 бегун за 1 час пробежал расстояние , равное дуге АВС ,
S(АВС)=(x+11)*1=(x+11) км . Это расстояние больше, чем один круг .
Разница расстояний равна S(BAC)=S(ABC)-S(AB)=(x+11)-x=11 км .
За 20 мин второй бегун пробежал расстояние, равное длине дуги
АС, S(AC)=(x+11) км/ч*20 мин=(x+11) км/ч*(20/60 часа)=(х+11)*(1/3) км .
S(BAC)=S(BA)+S(AC)=4+(x+11)*(1/3)=11

ответ: скорость 1 бегуна = 11 км/ч .

Разложим левую часть неравенства на множители по формуле разности квадратов.
Нули функции: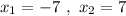 .
.
Решим методом интервалов. Подсчитаем знаки на образовавшихся промежутках.
Выбираем интервалы, где функция положительна.