
Задание 1
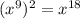
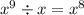
Задание 2
2
Объяснение:
Задание 1
Формулы:

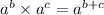
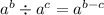
Поэтому,
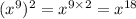
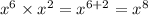
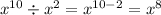
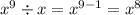
Задание 2
Надо найти последнюю цифру числа 2^53. Двойка 53 раза умножается на саму себя. Найдем закономерность (смотрим на последнюю цифру):
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1024
...
Последние цифры идут в таком порядке: 2, 4, 8, 6.
Остаток от деления степени на 4 равен 1 => последняя цифра 2Остаток от деления степени на 4 равен 2 => последняя цифра 4Остаток от деления степени на 4 равен 3 => последняя цифра 8Остаток от деления степени на 4 равен 0 => последняя цифра 653 mod 4 = 1 => последняя цифра 2.
ответ: А) 1
Объяснение:
a₂ = a₁ + d
a₃ = a₁ + 2d
Складемо систему рівнянь:
{a₁ + a₂ + a₃ = 2
{a₁² + a₂² + a₃² = 14/9
{a₁ + a₁ + d + a₁ + 2d = 2
{3a₁ + 3d = 2 | :3
{a₁ + d = 2/3
a₂ = 2/3
Підставимо у друге рівняння a₂ = 2/3
{a₁² + (2/3)²+ a₃² = 14/9
{a₁² + 4/9 + a₃² = 14/9
a₁² + a₃² = 14/9 - 4/9
a₁² + a₃² = 10/9
a₁² + (a₁ + 2d)² = 10/9
a₁² + a₁² + 4a₁d + 4d² = 10/9
2a₁² + 4a₁d + 4d² = 10/9 | :2
a₁² + 2a₁d + 2d₁² = 5/9
a₁² + 2a₁d + d² + d² = 5/9
(a₁ + d)² + d² = 5/9
a₂² + d² = 5/9
(2/3)² + d² = 5/9
4/9 + d² = 5/9
d² = 5/9 - 4/9
d² = 1/9
d = ± 1/3
Звідси знайдемо третій член прогресії:
d = 1/3
a₁ = a₂ - d = 2/3 - 1/3 = 1/3
a₃ = a₁ + 2d = 1/3 + 2 * 1/3 = 1/3 + 2/3 = 3/3 = 1
-3 <= x <= 11 |•5
-15 <= 5x <= 55 |+1
-14 <= 5x+1 <= 56 |:2
-7 <= (5x+1)/2 <= 28
E(y): [-7; 28]