Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы . С другой стороны, как нетрудно заметить, их сумма равна . Стало быть, каждый из них равен единице:
Детерминант (-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: , откуда должно делиться на , а должно делиться на . Тогда , потому . Из первого , а из второго -- . Итак, , поэтому решение переписывается в виде . Итак, слева у исходного неравенства стоит нуль, а справа -- . Получаем, что , а потому подходит только и соответствующая тройка .
При сложении\вычитании комплексных чисел в поле комплексных чисел, отдельно складываем действительную и мнимую части. Умножение комплексных чисел производится также, как произведение скобки на скобку в поле действительных чисел. При этом при перемножении появляется квадрат числа i, который, как известно, в поле комплексных чисел равен Минус единице.
Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы . С другой стороны, как нетрудно заметить, их сумма равна
. С другой стороны, как нетрудно заметить, их сумма равна 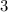 . Стало быть, каждый из них равен единице:
. Стало быть, каждый из них равен единице: 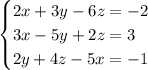
Детерминант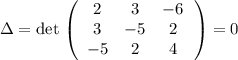 (-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать:
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 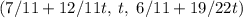 , откуда
, откуда 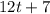 должно делиться на
должно делиться на  , а
, а 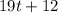 должно делиться на
должно делиться на 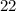 . Тогда
. Тогда 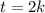 , потому
, потому 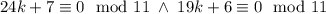 . Из первого
. Из первого 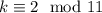 , а из второго --
, а из второго -- 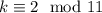 . Итак,
. Итак, 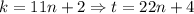 , поэтому решение переписывается в виде
, поэтому решение переписывается в виде 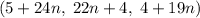 . Итак, слева у исходного неравенства стоит нуль, а справа --
. Итак, слева у исходного неравенства стоит нуль, а справа -- 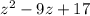 . Получаем, что
. Получаем, что 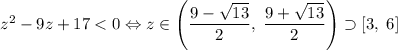 , а потому подходит только
, а потому подходит только 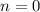 и соответствующая тройка
и соответствующая тройка 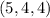 .
.