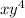Общий ход построения данных графиков: График - прямая, для построения требуется две точки. Чертим координатную плоскость, подписываем оси и отмечаем положительное направление стрелками: вправо по оси х и вверх по оси у. Отмечаем центр – точку О и единичные отрезки по обеим осям в 1 клетку. Далее заполняем таблицу (для каждого графика свою, приведена ниже): Х= У= Отмечаем точки в системе координат, проводим через них прямую. Подписываем график. Всё! Итак, начнём:
у=-4х - прямая, проходящая через начало координат , поэтому достаточно ещё одной точки, например х=1, у= -4 , ставим точку (1;-4) и проводим прямую через эту точку и начало координат.
Алгоритм поиска. Ищем точки экстремума по условию y'=0. Определяем, является ли точка минимумом или максимумом по критерию изменения знака y' в данной точке: если знак y' изменяется с "+" на "-", то функция имеет максимум; если с "-" на "+" - минимум; если не изменяется - не является экстремумом. Наибольшее значение на отрезке определяется как максимальное значение среди всех максимумов функции на отрезке и значений функции на концах отрезка. Наименьшее значение функции определяется как минимальное значение среди всех минимумов на отрезке и значений функции на концах отрезка.
y'=3x²-6x=3x(x-2). Точки, подозрительные на экстремум: x=0; x=2. При x∈(0;2) y'<0 (функция y убывает (y↓)), при x∉(0;2) y'>0 (функция y возрастает (y↑)). y(0) = 0 y(2) = 2³-3*2² = 8-12 = -4
Слева от точки (0;0) функция y возрастающая, справа - убывающая. Значит, точка (0;0) является локальным максимумом. Слева от точки (2;-4) функция y убывающая, справа - возрастающая. Значит, точка (2;-4) является локальным минимумом.
Наибольшее значение функции y на отрезке [-1;3] равно max (y(-1),y(0),y(3)) = max (-4,0,0) = 0 (достигается в точках x=0 и x=3. Наименьшее значение функции y на отрезке [-1;3] равно min (y(-1),y(2),y(3)) = min (-4,-4,0) = -4 (достигается в точках x=-1 и x=2.
1) y³
2)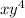
Объяснение:
1) В первой части равенства вынесем за скобки x, а во второй -- xy³
*·x(x²-y) = xy³(x²-y)
Видим, что * -- это y³
2) Первую часть равенства оставляем без изменений, а во второй за скобки вынесем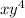
(x-1)·* =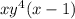
Видим, что * -- это