Это тождество Эйлера, являющееся частным случаем формулы Эйлера при .
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма (алгебра);
2) отношение длины окружности к ее диаметру (геометрия);
3) мнимую единицу (комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".
Решим второе неравенство _____-6_________-1_______ + - + и Найдем пересечение решений ответ: и 2. ( я нашла корни по теореме Виета) _____-2______-1________ + - + ответ: и Решим первое неравенство, найдем корни, приравняв нулю. Разложим на множители 1 неравенство Отметим точки на числовой прямой, причем -2-закрашенная, а 4 и - 4 выколотые( исключены вторым неравенством) ______-4______-2_____4________ + - + + Знаки ставятся справа налево начиная с +. Тк (х-4)^2, то на следующем промежутке знак не поменяется, далее чередуются -, + ООФ
Решим второе неравенство _____-6_________-1_______ + - + и Найдем пересечение решений ответ: и 2. ( я нашла корни по теореме Виета) _____-2______-1________ + - + ответ: и Решим первое неравенство, найдем корни, приравняв нулю. Разложим на множители 1 неравенство Отметим точки на числовой прямой, причем -2-закрашенная, а 4 и - 4 выколотые( исключены вторым неравенством) ______-4______-2_____4________ + - + + Знаки ставятся справа налево начиная с +. Тк (х-4)^2, то на следующем промежутке знак не поменяется, далее чередуются -, + ООФ
Это тождество Эйлера, являющееся частным случаем формулы Эйлера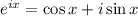 при
при  .
.
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма (алгебра);
(алгебра);
2) отношение длины окружности к ее диаметру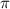 (геометрия);
(геометрия);
3) мнимую единицу (комплексные числа);
(комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".