
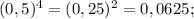
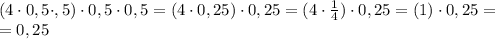
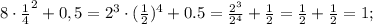
Объяснение:
у=-3х²+8х+3
Данным графиком будет являться параболла.
1.Чтобы быстро и эффективно все решить найдем координаты вершин параболы:
1)x0=-b/2a=-8/-6=1.3...
2)yo=-D/4a=-10/-12=0.83...
a=-3
b=8
-b=-8
c=3
D=b2-4ac
D=64-4*(-3)*3=64+36=100 И КОРЕНЬ РАВЕН 10
X1=-b+кореньD/2A=-8+10/-6=-1/3
X2=ТОЖЕ САМОЕ НО С -. -8-10/-6=3
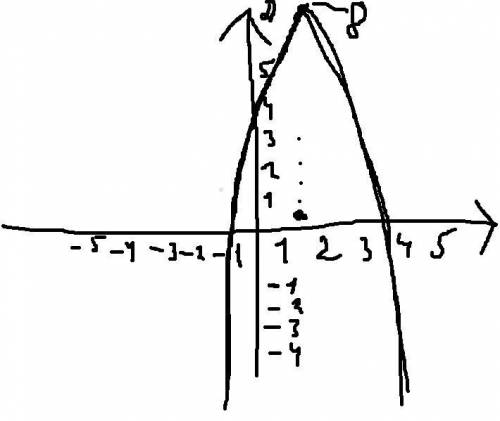
2.Строим график
Возьмем пару точек
x 1 0 -1
y 8 0 -8
И отмечаем на граффике, это сможите сами сделать. А суммарно ветви параболы уйдут вниз так как -3 и график будет выглядить вот так:
А 2 уравнение вы не поймете там с корнями!
3)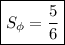 квадратных единиц
квадратных единиц
4)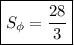 квадратных единиц
квадратных единиц
Объяснение:
3)
По условию фигура ограничена линиями:
Линии ограничивают область (закрашенную желтым цветом и которую можно назвать ABC).
Прямые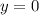 и
и 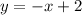 имеют пересечения в точке C(2;0).
имеют пересечения в точке C(2;0).
0 = -x + 2 ⇒ x = 2; y(-2) = 0
Прямые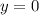 и
и  имеют пересечения в точке A(0;0).
имеют пересечения в точке A(0;0).
Прямые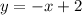 и
и  имеют пересечения в точке B(0;0).
имеют пересечения в точке B(0;0).
Однако так как нас согласно расположению графиков относительно друг друг друга, то нас интересует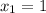 , то есть точка B(1;1).
, то есть точка B(1;1).
Проведем прямую x = 1. Таким образом она разбила желтую часть на две фигуры. Где площадь криволинейно трапеции ABD с пределами интегрирования от 0 до 1 можно найти с определенного интеграла, а оставшуюся площадь, как площадь треугольника BDC. То есть площадь фигуры имеет вид: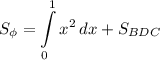 .
.
а)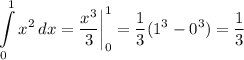 квадратных единиц.
квадратных единиц.
б)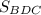
Так как отрезок BD треугольника ΔBDC лежит на прямой x = 1, то треугольник ΔBCD - прямоугольный с катетами BD и DC.
Зная координаты точек B(1;1),D(1;0),C(2;0) найдем длинны отрезков BD и DC.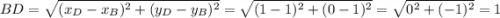 .
.
По формуле площади прямоугольного треугольника (ΔBDC) :
в) Площадь фигуры: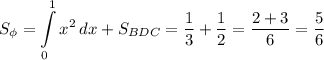 квадратных единиц.
квадратных единиц.
4)
По условию фигура ограничена линиями:
Пределы интегрирования:
Найдем площадь криволинейной трапеции по определению: