
В решении.
Объяснение:
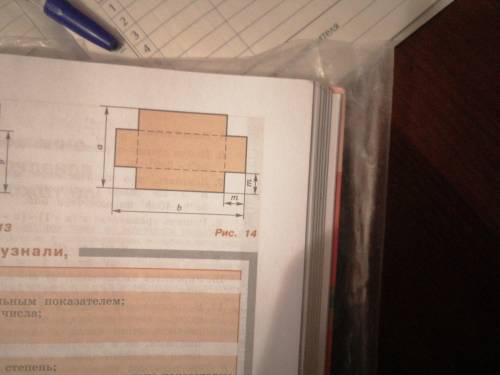
1) BH = a + b;
AB = a - b + b = a;
AD = a;
HL = a - b;
ML = b;
MD = b;
P = a + b + a + a + a - b + b + b = 4a + 2b = 2(2a + b);
2) Р = 8*m + 2(b - 2m) + 2(a - 2m) =
= 8m + 2b - 4m + 2a - 4m =
= 2a + 2b = 2(a + b).
Из левой части получим правую для чего домножим числитель и знаменатель левой части на сумму (sinα+cosα)
((sinα+cosα)²)/((cosα-sinα)(sinα+cosα)) Числитель разложим по формуле
(а+в)²=а²+2ав+в², а знаменатель по формуле (а-в)*(а+в)=а²- в², и почленно разделим числитель на знаменатель, предварительно применив формулу косинуса двойного аргумента cos²α-sin²α=cos2α; синуса двойного аргумента 2sinα*cosα= sin2α и основное тригонометрическое тождество sinα²+cos²α=1.
(sinα²+2sinα*cosα+cos²α)/(cos²α-sin²α)=(1+sin2α)/(cos2α)=
1/cos2α+(sin2α)/(cos2α)=tg2α+(1/cos2α) , что и требовалось доказать.
1) 3a + 2b
2) 2(a + b - 4m)
Объяснение:
a + b + (a-b) + b + b + a = a + b + a -b + b + b + a = 3a + 2b
a - 2m + b - 2m + a - 2m + b - 2m = 2a + 2b - 8m = 2(a + b - 4m)
:)