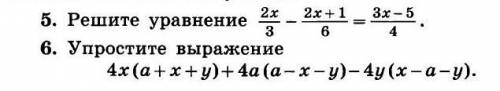
Алгебра: Решите уравнение. Сделайте !

Решите уравнение. Сделайте !

👇

Ответ:

Goodok10

13.12.2021

№5.

В таком уравнении следует избавляться от дробей, приводя их к общему знаменателю. Приведя, мы сможем убрать знаменатели и оставить числители.

2х/3 - (2х+1)/6 = (3х-5)/4

Наименьший общий знаменатель - 12.

8х/12 - (4х+2)/12 = (9х-15)/12

Убираем знаменатели.

8х-(4х+2) = 9х-15

8х-4х-2 = 9х-15

8х-4х-9х = -15+2

-5х = -13

х = -13/-5 = 13/5 = 2 3/5 = 2,6

х = 2,6

№6.

4х(а+х+у)+4а(а-х-у)-4у(х-а-у) = 4ах+4х²+4ху+4а²-4ах-4ау-4ху+4ау+4у² = 4х²+4а²+4у² = 4(х²+а²+у²)

4,8(77 оценок)

Ответ:

anonymous18

13.12.2021

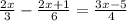
$\frac{2x}{3}-\frac{2x+1}{6}=\frac{3x-5}{4}$

Домножаем до общего знаменателя 12

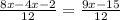
$\frac{8x-4x-2}{12}=\frac{9x-15}{12}$

Убираем 12

8x-4x-2=9x-15

8x-4x-9x=2-15

-5x=-13

x=2,6

4x(a+x+y)+4a(a-x-y)-4y(x-a-y)

4xa+4x^2+4xy+4a^2-4ax-4ay-4yx+4ay+4y^2

Зачёркиваем слагаемые с одинаковыми буквами

4х^2+4a^2+4у^2

4(x^2+y^2+a^2)

4,6(18 оценок)

Открыть все ответы

Ответ:

hjhytu

13.12.2021

По определению, 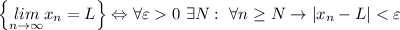$\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 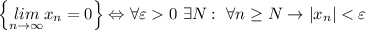$\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

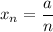
2) $x_n=\dfrac{a}{n}$

|x_n|

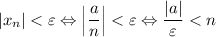
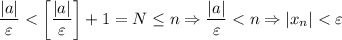
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

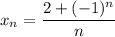
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

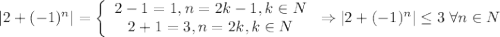
$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда 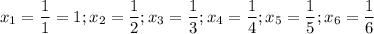$x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 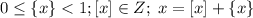$0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

4,6(34 оценок)

Ответ:

dana085

13.12.2021

Многочлен стандартного вида - это многочлен, в котором все слагаемые имеют стандартный вид и в котором приведены подобные слагаемые (имеют одинаковую буквенную часть).

Степень многочлена - это степень наибольшего одночлена, в ходящего в многочлен.

1) 22а² - 40а³ + 18а² + 29а³ + а⁴ = а⁴ - 11а³ + 40а²; степень - 4;

2) -7b⁵ - 13b⁶ + 15 - 9b⁵ + 34b⁶ = 21b⁶ - 16b⁵ + 15; степень - 6;

3) 41c² + 62c³ - 99 - 42c² + 38c³ = 100c³ - c² - 99; степень - 3;

4) -52k + k⁴ - 18k⁴ + 52 - k = -17k⁴ - 53k + 52; степень - 4.

4,5(89 оценок)

Это интересно:

Взаимоотношения

17.05.2021

Как правильно флиртовать с Раками: знак зодиака и любовные отношения...

Дом-и-сад

09.03.2020