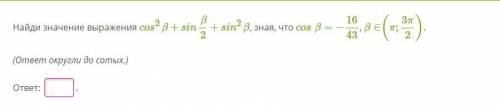
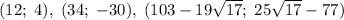
Объяснение:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt[6]{(x+y)^3(x-y)^2}=8](/tpl/images/1358/0734/79d4c.png)
Выполним преобразование:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=8](/tpl/images/1358/0734/48821.png)
или ![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8](/tpl/images/1358/0734/9c2ec.png)
Пусть ![\sqrt{x+y}=k,\;\sqrt[3]{x-y}=t](/tpl/images/1358/0734/e7517.png)
.
Тогда для 1-ого случая:
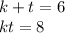
Заметим здесь теорему Виета (если не заметили, то можно просто решить эту систему).
Тогда:
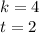
или
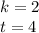
Замечу, что замену можно было не делать. Она дана для понимания. Можно было сразу написать то, что идет после слов обратная замена.
Обратная замена:
![1)\\\sqrt{x+y}=4\\\sqrt[3]{x-y}=2](/tpl/images/1358/0734/fbf65.png)
Первое уравнение можно возвести в квадрат, так как обе части его положительны:
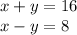
Очевиден прием решения: сложение.
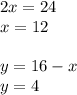
Получили пару чисел (12; 4).
![2)\\\sqrt{x+y}=2\\\sqrt[3]{x-y}=4\\\\x+y=4\\x-y=64\\\\2x=68\\x=34\\\\y=4-x\\y=-30](/tpl/images/1358/0734/7b359.png)
Получили пару (34; -30).
Для 2-ого случая:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8\\\\\sqrt{x+y}=3+\sqrt{17}\\\sqrt[3]{x-y}=3-\sqrt{17}\\\\x+y=(3+\sqrt{17})^2\\x-y=(3-\sqrt{17})^3\\\\x=103-19\sqrt{17}\\y=25\sqrt{17}-77](/tpl/images/1358/0734/218c4.png)
Еще одна пара чисел: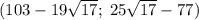 
Заметим, что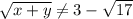 
, т.к. это число меньше 0.
Система уравнений решена!
Объяснение:
1. Пусть на одном складе было х тонн картошки.
2. Тогда на другом складе было 2,5х тонн картошки.
3. На одном складе стало (х + 72) тонн картошки.
4. На другом складе стало (2,5х + 30) тонн картошки.
5. Составим уравнение и узнаем сколько картошки было на втором складе первоначально, если в итоге на обоих складах картошки стало поровну.
х + 72 = 2,5х + 30;
72 - 30 = 2,5х - х;
1,5х = 42;
х = 42 : 1,5;
х = 28 тонн - картошки на одном складе.
6. 28 * 2,5 = 70 тонн - картошки на другом складе
ответ: На одном складе было первоначально 28 тонн картошки, а на другом 70 тонн.