Question

на первой фотку нужно найти производные сложных функций ,на второй вычислить пределы последовательностей , буду очень благодарна

Answer 1

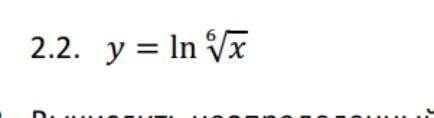
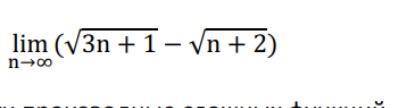
$1)\ \ y=ln\sqrt[6]{x}\ \ \ ,\ \ \ \ \ \boxed{\ (lnu)'=\dfrac{1}{u}\cdot u'}\ \ ,\ \ u=\sqrt[6]{x}\ ,\\\\\\y'=\dfrac{1}{\sqrt[6]{x}}\cdot (\sqrt[6]{x} )'=\dfrac{1}{\sqrt[6]{x}}\cdot \dfrac{1}{6}\cdot x^{\frac{1}{6}-1}=\dfrac{1}{\sqrt[6]{x}}\cdot \dfrac{1}{6}\cdot x^{-\frac{5}{6}}=\dfrac{1}{\sqrt[6]{x}\cdot \ 6\, \sqrt[6]{x^5}}=\dfrac{1}{6x}$

$2)\ \ \lim\limits_{n \to \infty}\Big(\sqrt{3n+1}-\sqrt{n+2}\Big)=\lim\limits_{n \to \infty}\dfrac{(\sqrt{3n+1}-\sqrt{n+2})(\sqrt{3n+1}+\sqrt{n+2})}{\sqrt{3n+1}+\sqrt{n+2}}=\\\\\\=\lim\limits_{n \to \infty}\dfrac{(3n+1)-(n+2)}{\sqrt{3n+1}+\sqrt{n+2}}=\lim\limits_{n \to \infty}\dfrac{2n-1}{\sqrt{3n+1}+\sqrt{n+2}}=\Big[\ \dfrac{:n}{:n}\ \Big]=$

$=\lim\limits_{n \to \infty}\dfrac{2-\dfrac{1}{n}}{\sqrt{\dfrac{3n+1}{n^2}}+\sqrt{\dfrac{n+2}{n^2}}}=\lim\limits_{n \to \infty}\dfrac{2-\dfrac{1}{n}}{\sqrt{\dfrac{3}{n}+\dfrac{1}{n^2}}+\sqrt{\dfrac{1}{n}+\dfrac{2}{n^2}}}=\\\\\\=\lim\limits_{n \to \infty}\dfrac{2-0}{0+0}=\Big[\ \dfrac{2}{0}\ \Big]=\infty$