Question

x²-2-x=0 графическое решение

Answer 1

(см. объяснение)

Объяснение:

Рассмотрим уравнение:

$x^2-x-2=0$

Введем функцию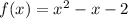 $f(x)=x^2-x-2$. Это парабола, ветви которой направлены вверх, а вершина имеет координаты $\left(\dfrac{1}{2};\;-\dfrac{9}{4}\right)$.

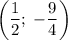Составим таблицу:

$\left\begin{array}{}x&|&-2&0&0.5&1&3\\y&|&4&-2&-2.25&-2&4\end{array}\right$

Построение:

(см. прикрепленный файл)

Видим, что наш эскиз параболы пересекает ось x приблизительно в точках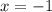 $x=-1$ и $x=2$.

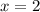Проверим это подстановкой в уравнение:

$x=-1:\\1+1-2=0\\0=0$                         $x=2:\\4-2-2=0\\0=0$

В обоих случаях получили верность.

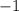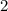Значит число $-1$ и $2$ - это корни исходного уравнения.

Задание выполнено!