Достове́рным собы́тием в теории вероятностей называется событие, которое в результате опыта или наблюдения непременно должно произойти. Обозначается символом. Для достоверного события, то есть вероятность события равна единице. Но, не всякое событие, вероятность которого равна 1, является достоверным
Два случайные события А и В называются противоположными, если они несовместны и образуют полную группу событий. Примеры: студент может сдать или не сдать экзамен, день и ночь. Конкретный результат испытания называется элементарным событием.
Формально говоря, элементарное событие — это подмножество исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент.
События A и B называются зависимыми, если вероятность одного из них зависит от того, произошло или не произошло другое событие.
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Полная группа событий По́лной гру́ппой(системой) собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно и только одно из них. Сумма вероятностей всех событий в группе всегда равна 1.
Какой формулой пользоваться значения не имеет. На фотографиях представлены решения уравнения 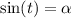 .
.
Если нарисовать числовую окружность, то значение 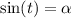 есть координата точки
есть координата точки 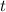 по оси
по оси 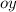 , ведь для любой точки числовой окружности справедливо, что
, ведь для любой точки числовой окружности справедливо, что 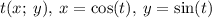 , т.е. точка
, т.е. точка 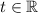 имеет координаты
имеет координаты 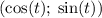 .
.
Если провести прямую, параллельную оси 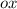 через точку
через точку 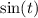 , то она пересечётся с числовой окружностью в каких-то точках.
, то она пересечётся с числовой окружностью в каких-то точках.
Чтобы было понятнее, советую нарисовать окружность радиусом 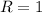 и центром в точке
и центром в точке 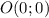 и отмечать всё, о чём я пишу.
и отмечать всё, о чём я пишу.
Теперь рассмотрим эти точки пересечения.
Если 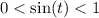 , то пересечения будут в первой и второй четвертях.
, то пересечения будут в первой и второй четвертях.
Если 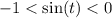 , то пересечения будут в третьей и четвёртой четвертях.
, то пересечения будут в третьей и четвёртой четвертях.
Если 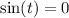 , то пересечений тоже два и это
, то пересечений тоже два и это 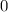 и
и 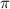 .
.
Если 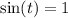 , то пересечение только одно, при чём точка пересечения будет и точкой касания, и равна она
, то пересечение только одно, при чём точка пересечения будет и точкой касания, и равна она 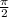 .
.
Если же 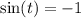 , то пересечение тоже одно, тоже является точкой касания, но значение равно
, то пересечение тоже одно, тоже является точкой касания, но значение равно 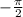 .
.
А теперь вспомним определение арксинуса. Арксинусом числа 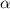 называют такой угол
называют такой угол 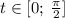 , что
, что 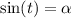 . Главное здесь то, что
. Главное здесь то, что 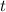 может быть углом только первой четверти.
может быть углом только первой четверти.
Отсюда же следует, что 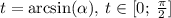 .
.
Это прекрасно работает для 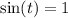 , ведь
, ведь 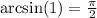 .
.
Но только недавно мы проверили, что у нас может быть и не одно, а два решения. Как поступить в случае, если арксинус работает только для углов первой четверти, а нам нужно, чтобы он работал во второй? ответ прост. 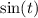 - это число, а
- это число, а 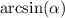 - угол.
- угол.
Пусть прямая 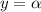 пересекается с окружностью в точках
пересекается с окружностью в точках 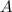 в первой четверти и
в первой четверти и 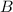 во второй четверти, а точку
во второй четверти, а точку 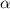 на оси
на оси 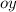 мы обзовём
мы обзовём 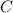 . Рассмотрим треугольники
. Рассмотрим треугольники 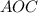 и
и 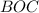 , в них:
, в них:
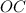 - отрезок, лежащий на оси
- отрезок, лежащий на оси 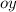 , а
, а 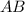 - хорда, параллельная оси
- хорда, параллельная оси 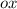 , значит
, значит 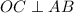 , по аксиоме о перпендикулярности прямых. Следовательно, треугольники
, по аксиоме о перпендикулярности прямых. Следовательно, треугольники 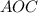 и
и 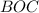 - прямоугольные по определению.
- прямоугольные по определению.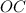 - отрезок, лежащий на радиусе и
- отрезок, лежащий на радиусе и 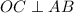 , значит
, значит 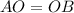 по свойству радиуса.
по свойству радиуса.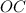 - общая сторона.
- общая сторона.Треугольники 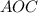 и
и 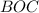 равны по двум катетам. Из этого следует и то, что их соответственные углы равны. Т.е. угол
равны по двум катетам. Из этого следует и то, что их соответственные углы равны. Т.е. угол 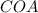 и угол
и угол 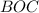 .
.
Но углы мы отсчитываем от точки  , обзовём её
, обзовём её 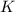 . Тогда угол
. Тогда угол 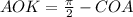 . А это угол
. А это угол 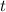 первой четверти.
первой четверти.

А угол 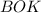 - искомый угол второй четверти.
- искомый угол второй четверти.
Как нам известно, все числа на числовой окружности получаются с поворота на определённый угол, пусть 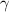 - этот угол. И если мы сделаем полный оборот, то мы хоть и придём в ту же самую точку, но вот число уже будет другое, ведь поворачивались мы на другой угол, равный
- этот угол. И если мы сделаем полный оборот, то мы хоть и придём в ту же самую точку, но вот число уже будет другое, ведь поворачивались мы на другой угол, равный 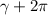 . Таким образом, чтобы описать все числа, находящиеся в точке на окружности с координатами
. Таким образом, чтобы описать все числа, находящиеся в точке на окружности с координатами 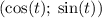 надо добавить
надо добавить 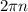 , где
, где 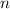 - целое (чтобы получились полные обороты).
- целое (чтобы получились полные обороты).
Вот так и получается первая формула.
Что до второй, то тут всё проще. Выводить её не буду, и так ответ уже километровый. В ней всё работает на чётности 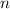 . Если
. Если 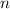 - чётное, то формула трансформируется в
- чётное, то формула трансформируется в 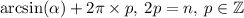 , если нечётное, то в
, если нечётное, то в 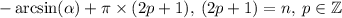 , ну а
, ну а 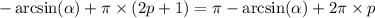 . Т.е. это тоже самое, только записанное в одну строчку. Использовать вторую формулу не советую. Она менее интуитивно понятная. Но если в ней разобраться, то решение уменьшается в размере, это правда.
. Т.е. это тоже самое, только записанное в одну строчку. Использовать вторую формулу не советую. Она менее интуитивно понятная. Но если в ней разобраться, то решение уменьшается в размере, это правда.
Как-то так. Фу-у-у-ух. Много. Очень Много Букв.
P.S. Прости за задержку.
7. 4,5,6 и т.д
8. 0,8; 0,9; 1; и т.д
9. 0,1,2