Question

1. Разность двух чисел равна 17, а их сумма равна - 9. Найди эти числа. 2. Сумма двух чисел равна 23, а их произведение равно 102. Найди эти числа.
3. Разность двух натуральных чисел равна 12, а их произведение равно 364. Найди эти числа.

Answer 1

1. пусть эти два числа будут a и b, тогда запишем систему

$\left \{ {{a-b = 17} \atop {a+b = 9}} \right.$

выявим а

$\left \{ {{a-b = 17} \atop {a = 9-b}} \right.$

подставляем a в первое выражение и получается

9 - b - b = 17

9 - 2b = 17

-2b = 17-9

-2b = 8

b = -4

и теперь значение b подставляем во второе выражение, чтобы найти a

a = 9 - (-4)

a = 9 + 4

a = 13

ответ: числа 13 и -4

2. пусть эти два числа будут a и b, тогда запишем систему

$\left \{ {{a+b = 23} \atop {a * b = 102}} \right.$

выявим a в первом выражении

a = 23-b

и теперь подставим это значение во второе выражение

(23-b)b = 102

23b-b^2 = 102

-b^2 + 23b -102 =0 --решаем квадратное уравнение через дискриминант

D = 529 -408= 121

1b =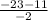 $\frac{-23-11}{-2}$ = 17              a=23-17=6

2b = $\frac{-23+11}{-2}$ = 6              a=23-6=17

ответ: числа 17 и 6

3. пусть эти два числа будут a и b, тогда запишем систему

$\left \{ {{a-b = 12} \atop {a * b= 364}} \right.$

выявим a в первом выражении

a = 12+b

и теперь подставим это значение во второе выражение

(12+b)b=364

b^2 + 12b =364

b^2 +12b - 364 = 0 --решаем квадратное уравнение через дискриминант

D= 144 + 1456= 1600

1b =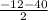 $\frac{-12-40}{2}$= -26          a=12-26=-14

2b =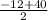 $\frac{-12+40}{2}$= 14           a=12+14=26

ответ: числа -26 и -14; 14 и 26